Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 58245 by tanmay last updated on 20/Apr/19

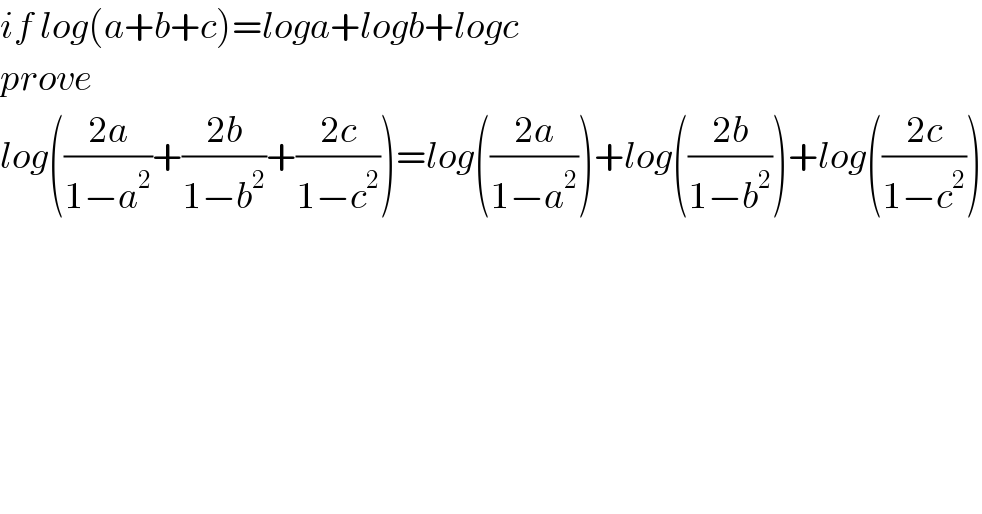
if log(a+b+c)=loga+logb+logc prove log(((2a)/(1−a^2 ))+((2b)/(1−b^2 ))+((2c)/(1−c^2 )))=log(((2a)/(1−a^2 )))+log(((2b)/(1−b^2 )))+log(((2c)/(1−c^2 )))

$${if}\:{log}\left({a}+{b}+{c}\right)={loga}+{logb}+{logc} \\ $$$${prove} \\ $$$${log}\left(\frac{\mathrm{2}{a}}{\mathrm{1}−{a}^{\mathrm{2}} }+\frac{\mathrm{2}{b}}{\mathrm{1}−{b}^{\mathrm{2}} }+\frac{\mathrm{2}{c}}{\mathrm{1}−{c}^{\mathrm{2}} }\right)={log}\left(\frac{\mathrm{2}{a}}{\mathrm{1}−{a}^{\mathrm{2}} }\right)+{log}\left(\frac{\mathrm{2}{b}}{\mathrm{1}−{b}^{\mathrm{2}} }\right)+{log}\left(\frac{\mathrm{2}{c}}{\mathrm{1}−{c}^{\mathrm{2}} }\right) \\ $$

Answered by Kunal12588 last updated on 20/Apr/19

log(a+b+c)=log a + log b + log c ⇒log(a+b+c)=log(abc) ⇒a+b+c=abc let a=tan α=t_1 , b=tan β=t_2 , c=tan γ=t_3 ∴ t_1 +t_2 +t_3 =t_1 t_2 t_3 ⇒t_1 +t_2 =−t_3 (1−t_1 t_2 ) ⇒−t_3 =((t_1 +t_2 )/(1−t_1 t_2 )) ⇒tan(π−γ)=tan(α+β) ⇒α+β+γ=π ⇒2α+2β+2γ=2π ⇒tan(2α+2β)=tan(2π−2γ) ⇒((tan 2α + tan 2β)/(1−tan 2α tan2β))=−tan 2γ ⇒tan 2α + tan 2β + tan 2γ = tan 2α tan2β tan 2γ ⇒log(((2t_1 )/(1−t_1 ^2 ))+((2t_2 )/(1−t_2 ^2 ))+((2t_3 )/(1−t_3 ^2 )))=log(((2t_1 )/(1−t_1 ^2 ))×((2t_2 )/(1−t_2 ^2 ))×((2t_3 )/(1−t_3 ^2 ))) ⇒log(((2a)/(1−a^2 ))+((2b)/(1−b^2 ))+((2c)/(1−c^2 )))=log(((2a)/(1−a^2 )))+log(((2b)/(1−b^2 )))+log(((2c)/(1−c^2 )))

$${log}\left({a}+{b}+{c}\right)={log}\:{a}\:+\:{log}\:{b}\:+\:{log}\:{c} \\ $$$$\Rightarrow{log}\left({a}+{b}+{c}\right)={log}\left({abc}\right) \\ $$$$\Rightarrow{a}+{b}+{c}={abc} \\ $$$${let}\:\:{a}={tan}\:\alpha={t}_{\mathrm{1}} ,\:\:{b}={tan}\:\beta={t}_{\mathrm{2}} ,\:\:{c}={tan}\:\gamma={t}_{\mathrm{3}} \\ $$$$\therefore\:\:{t}_{\mathrm{1}} +{t}_{\mathrm{2}} +{t}_{\mathrm{3}} ={t}_{\mathrm{1}} {t}_{\mathrm{2}} {t}_{\mathrm{3}} \\ $$$$\Rightarrow{t}_{\mathrm{1}} +{t}_{\mathrm{2}} =−{t}_{\mathrm{3}} \left(\mathrm{1}−{t}_{\mathrm{1}} {t}_{\mathrm{2}} \right) \\ $$$$\Rightarrow−{t}_{\mathrm{3}} =\frac{{t}_{\mathrm{1}} +{t}_{\mathrm{2}} }{\mathrm{1}−{t}_{\mathrm{1}} {t}_{\mathrm{2}} } \\ $$$$\Rightarrow{tan}\left(\pi−\gamma\right)={tan}\left(\alpha+\beta\right) \\ $$$$\Rightarrow\alpha+\beta+\gamma=\pi \\ $$$$\Rightarrow\mathrm{2}\alpha+\mathrm{2}\beta+\mathrm{2}\gamma=\mathrm{2}\pi \\ $$$$\Rightarrow{tan}\left(\mathrm{2}\alpha+\mathrm{2}\beta\right)={tan}\left(\mathrm{2}\pi−\mathrm{2}\gamma\right) \\ $$$$\Rightarrow\frac{{tan}\:\mathrm{2}\alpha\:+\:{tan}\:\mathrm{2}\beta}{\mathrm{1}−{tan}\:\mathrm{2}\alpha\:{tan}\mathrm{2}\beta}=−{tan}\:\mathrm{2}\gamma \\ $$$$\Rightarrow{tan}\:\mathrm{2}\alpha\:+\:{tan}\:\mathrm{2}\beta\:+\:{tan}\:\mathrm{2}\gamma\:=\:{tan}\:\mathrm{2}\alpha\:{tan}\mathrm{2}\beta\:\:{tan}\:\mathrm{2}\gamma \\ $$$$\Rightarrow{log}\left(\frac{\mathrm{2}{t}_{\mathrm{1}} }{\mathrm{1}−{t}_{\mathrm{1}} ^{\mathrm{2}} }+\frac{\mathrm{2}{t}_{\mathrm{2}} }{\mathrm{1}−{t}_{\mathrm{2}} ^{\mathrm{2}} }+\frac{\mathrm{2}{t}_{\mathrm{3}} }{\mathrm{1}−{t}_{\mathrm{3}} ^{\mathrm{2}} }\right)={log}\left(\frac{\mathrm{2}{t}_{\mathrm{1}} }{\mathrm{1}−{t}_{\mathrm{1}} ^{\mathrm{2}} }×\frac{\mathrm{2}{t}_{\mathrm{2}} }{\mathrm{1}−{t}_{\mathrm{2}} ^{\mathrm{2}} }×\frac{\mathrm{2}{t}_{\mathrm{3}} }{\mathrm{1}−{t}_{\mathrm{3}} ^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{log}\left(\frac{\mathrm{2}{a}}{\mathrm{1}−{a}^{\mathrm{2}} }+\frac{\mathrm{2}{b}}{\mathrm{1}−{b}^{\mathrm{2}} }+\frac{\mathrm{2}{c}}{\mathrm{1}−{c}^{\mathrm{2}} }\right)={log}\left(\frac{\mathrm{2}{a}}{\mathrm{1}−{a}^{\mathrm{2}} }\right)+{log}\left(\frac{\mathrm{2}{b}}{\mathrm{1}−{b}^{\mathrm{2}} }\right)+{log}\left(\frac{\mathrm{2}{c}}{\mathrm{1}−{c}^{\mathrm{2}} }\right) \\ $$

Commented by tanmay last updated on 20/Apr/19

bah! very good excellent...

$${bah}!\:{very}\:{good}\:{excellent}... \\ $$

Commented by Kunal12588 last updated on 20/Apr/19

Thank you sir ��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com