
Question Number 204360 by esmaeil last updated on 14/Feb/24
![if lim_(x→+∞) [(((a+6)x+1)/(ax+1))]=2→ find the largest and smallest correct value for a.](Q204360.png)
$${if} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left[\frac{\left({a}+\mathrm{6}\right){x}+\mathrm{1}}{{ax}+\mathrm{1}}\right]=\mathrm{2}\rightarrow \\ $$$${find}\:{the}\:{largest}\:{and}\:{smallest}\:{correct} \\ $$$${value}\:{for}\:{a}. \\ $$
Answered by deleteduser1 last updated on 14/Feb/24
![=lim_(x→+∞) [((a+6+(1/x))/(a+(1/x)))]=((a+6)/a)=2⇒a=6](Q204362.png)
$$=\underset{{x}\rightarrow+\infty} {{lim}}\left[\frac{{a}+\mathrm{6}+\frac{\mathrm{1}}{{x}}}{{a}+\frac{\mathrm{1}}{{x}}}\right]=\frac{{a}+\mathrm{6}}{{a}}=\mathrm{2}\Rightarrow{a}=\mathrm{6} \\ $$
Commented by esmaeil last updated on 14/Feb/24
$${thank}\:\:{you}.\:\:{and}\:{smallest}\:{value}? \\ $$
Commented by esmaeil last updated on 14/Feb/24

$$\mathrm{2}\leqslant\frac{{a}+\mathrm{6}}{{a}}<\mathrm{3}\rightarrow\mathrm{1}\leqslant\frac{\mathrm{6}}{{a}}\langle\mathrm{2}\rightarrow \\ $$$$\mathrm{3}<{a}\leqslant\mathrm{6}\rightarrow\begin{cases}{{a}_{{l}} =\mathrm{6}}\\{{a}_{{s}} =\mathrm{4}\:\:\left({a}\:{is}\:{correct}\right)}\end{cases} \\ $$$$ \\ $$$$ \\ $$
Commented by esmaeil last updated on 14/Feb/24
![[((10)/4)]=2](Q204368.png)
$$\left[\frac{\mathrm{10}}{\mathrm{4}}\right]=\mathrm{2} \\ $$$$ \\ $$
Commented by deleteduser1 last updated on 15/Feb/24
![I thought [ ] was just a bracket,if [x] is floor of x, then [((a+6)/a)]=2<((a+6)/a)≤3⇒3≤a<6 ⇒min(a)=3 and upper bound of a=6](Q204369.png)
$${I}\:{thought}\:\left[\:\right]\:{was}\:{just}\:{a}\:{bracket},{if}\:\left[{x}\right]\:{is}\:{floor}\:{of} \\ $$$${x},\:{then}\:\left[\frac{{a}+\mathrm{6}}{{a}}\right]=\mathrm{2}<\frac{{a}+\mathrm{6}}{{a}}\leqslant\mathrm{3}\Rightarrow\mathrm{3}\leqslant{a}<\mathrm{6} \\ $$$$\Rightarrow{min}\left({a}\right)=\mathrm{3}\:{and}\:{upper}\:{bound}\:{of}\:{a}=\mathrm{6} \\ $$
Answered by mr W last updated on 15/Feb/24
![let t=(1/x) x→+∞ ⇒t→0^+ lim_(x→+∞) [(((a+6)x+1)/(ax+1))] =lim_(t→0^+ ) [((a+6+t)/(a+t))]=2 ⇒2<((a+6)/a)≤3 ⇒3≤a<6](Q204370.png)
$${let}\:{t}=\frac{\mathrm{1}}{{x}} \\ $$$${x}\rightarrow+\infty\:\Rightarrow{t}\rightarrow\mathrm{0}^{+} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left[\frac{\left({a}+\mathrm{6}\right){x}+\mathrm{1}}{{ax}+\mathrm{1}}\right] \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left[\frac{{a}+\mathrm{6}+{t}}{{a}+{t}}\right]=\mathrm{2} \\ $$$$\Rightarrow\mathrm{2}<\frac{{a}+\mathrm{6}}{{a}}\leqslant\mathrm{3} \\ $$$$\Rightarrow\mathrm{3}\leqslant{a}<\mathrm{6} \\ $$
Commented by deleteduser1 last updated on 14/Feb/24
![It seems 6 doesn′t work. a=6⇒lim_(x→+∞) [((12x+1)/(6x+1))]=lim_(x→+∞) [((2(6x+1)−1)/(6x+1))] =lim_(x→+∞) [2−(1/(6x+1))]=1,since 1<2−(1/(6x+1))<2 as x→+∞. Even though lim_(x→+∞) 2−(1/(6x+1))=2, it approaches 2 from the negative axis(2^− ),so all values are less than 2.](Q204377.png)
$${It}\:{seems}\:\mathrm{6}\:{doesn}'{t}\:{work}. \\ $$$${a}=\mathrm{6}\Rightarrow\underset{{x}\rightarrow+\infty} {{lim}}\left[\frac{\mathrm{12}{x}+\mathrm{1}}{\mathrm{6}{x}+\mathrm{1}}\right]=\underset{{x}\rightarrow+\infty} {{lim}}\left[\frac{\mathrm{2}\left(\mathrm{6}{x}+\mathrm{1}\right)−\mathrm{1}}{\mathrm{6}{x}+\mathrm{1}}\right] \\ $$$$=\underset{{x}\rightarrow+\infty} {{lim}}\left[\mathrm{2}−\frac{\mathrm{1}}{\mathrm{6}{x}+\mathrm{1}}\right]=\mathrm{1},{since}\:\mathrm{1}<\mathrm{2}−\frac{\mathrm{1}}{\mathrm{6}{x}+\mathrm{1}}<\mathrm{2}\:{as} \\ $$$${x}\rightarrow+\infty. \\ $$$${Even}\:{though}\:\underset{{x}\rightarrow+\infty} {{lim}}\mathrm{2}−\frac{\mathrm{1}}{\mathrm{6}{x}+\mathrm{1}}=\mathrm{2},\:{it}\:{approaches}\:\mathrm{2} \\ $$$${from}\:{the}\:{negative}\:{axis}\left(\mathrm{2}^{−} \right),{so}\:{all}\:{values}\:{are}\: \\ $$$${less}\:{than}\:\mathrm{2}. \\ $$
Commented by mr W last updated on 14/Feb/24
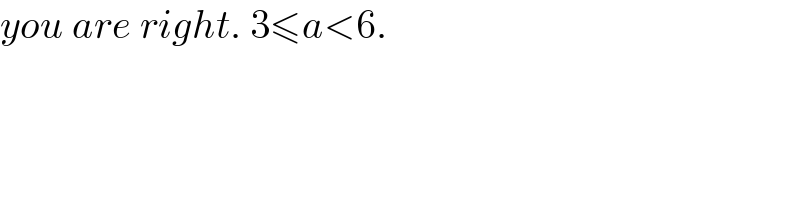
$${you}\:{are}\:{right}.\:\mathrm{3}\leqslant{a}<\mathrm{6}. \\ $$
Answered by deleteduser1 last updated on 14/Feb/24
![lim_(x→+∞) [((ax+1+6x)/(ax+1))]=lim_(x→+∞) [((6x)/(ax+1))+1]=2 If 6x<ax+1,then ((6x)/(ax+1))<1⇒[((6x)/(ax+1))+1]<2 ⇒6x≥ax+1⇒a≤((6x−1)/x)=6−(1/x)<6 a<6⇒[((6x)/(ax+1))+1]=[((ax+1+(6−a)x−1)/(ax+1))+1] =[2+(((6−a)x−1)/(ax+1))] lim_(x→+∞) (((6−a)x−1)/(ax+1))=((6−a)/a)=(6/a)−1 lim_(x→+∞) [((ax+1+6x)/(ax+1))]=lim_(x→+∞) [2+(((6−a)x−1)/(ax+1))]=2 lim_(x→+∞) (((6−a)x−1)/(ax+1))≤1⇒(6/a)−1≤1⇒a≥3 ⇒3≤a<6](Q204375.png)
$$\underset{{x}\rightarrow+\infty} {{lim}}\left[\frac{{ax}+\mathrm{1}+\mathrm{6}{x}}{{ax}+\mathrm{1}}\right]=\underset{{x}\rightarrow+\infty} {{lim}}\left[\frac{\mathrm{6}{x}}{{ax}+\mathrm{1}}+\mathrm{1}\right]=\mathrm{2} \\ $$$${If}\:\mathrm{6}{x}<{ax}+\mathrm{1},{then}\:\frac{\mathrm{6}{x}}{{ax}+\mathrm{1}}<\mathrm{1}\Rightarrow\left[\frac{\mathrm{6}{x}}{{ax}+\mathrm{1}}+\mathrm{1}\right]<\mathrm{2} \\ $$$$\Rightarrow\mathrm{6}{x}\geqslant{ax}+\mathrm{1}\Rightarrow{a}\leqslant\frac{\mathrm{6}{x}−\mathrm{1}}{{x}}=\mathrm{6}−\frac{\mathrm{1}}{{x}}<\mathrm{6}\: \\ $$$${a}<\mathrm{6}\Rightarrow\left[\frac{\mathrm{6}{x}}{{ax}+\mathrm{1}}+\mathrm{1}\right]=\left[\frac{{ax}+\mathrm{1}+\left(\mathrm{6}−{a}\right){x}−\mathrm{1}}{{ax}+\mathrm{1}}+\mathrm{1}\right] \\ $$$$=\left[\mathrm{2}+\frac{\left(\mathrm{6}−{a}\right){x}−\mathrm{1}}{{ax}+\mathrm{1}}\right] \\ $$$$\underset{{x}\rightarrow+\infty} {{lim}}\frac{\left(\mathrm{6}−{a}\right){x}−\mathrm{1}}{{ax}+\mathrm{1}}=\frac{\mathrm{6}−{a}}{{a}}=\frac{\mathrm{6}}{{a}}−\mathrm{1} \\ $$$$\underset{{x}\rightarrow+\infty} {{lim}}\left[\frac{{ax}+\mathrm{1}+\mathrm{6}{x}}{{ax}+\mathrm{1}}\right]=\underset{{x}\rightarrow+\infty} {{lim}}\left[\mathrm{2}+\frac{\left(\mathrm{6}−{a}\right){x}−\mathrm{1}}{{ax}+\mathrm{1}}\right]=\mathrm{2} \\ $$$$\underset{{x}\rightarrow+\infty} {{lim}}\frac{\left(\mathrm{6}−{a}\right){x}−\mathrm{1}}{{ax}+\mathrm{1}}\leqslant\mathrm{1}\Rightarrow\frac{\mathrm{6}}{{a}}−\mathrm{1}\leqslant\mathrm{1}\Rightarrow{a}\geqslant\mathrm{3} \\ $$$$\Rightarrow\mathrm{3}\leqslant{a}<\mathrm{6} \\ $$
