
Question Number 145851 by mathdanisur last updated on 08/Jul/21
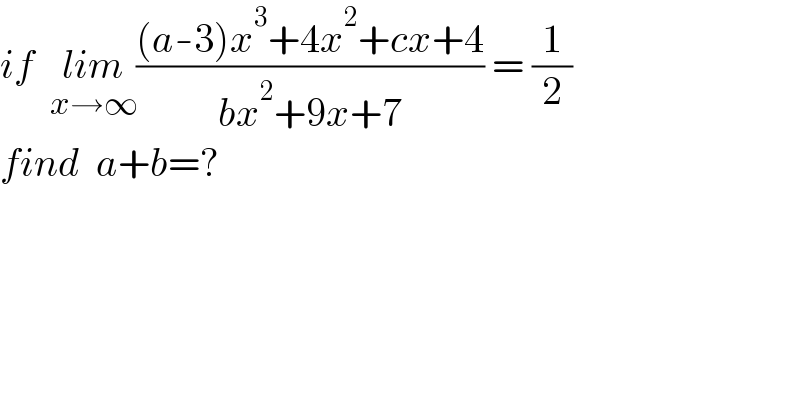
$${if}\:\:\underset{{x}\rightarrow\infty} {{lim}}\frac{\left({a}-\mathrm{3}\right){x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +{cx}+\mathrm{4}}{{bx}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{7}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${find}\:\:{a}+{b}=? \\ $$
Answered by Olaf_Thorendsen last updated on 08/Jul/21

$${a}−\mathrm{3}\:=\:\mathrm{0}\:\Rightarrow\:{a}\:=\:\mathrm{3} \\ $$$$\frac{\mathrm{4}}{{b}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{b}\:=\:\mathrm{8} \\ $$$${a}+{b}\:=\:\mathrm{11} \\ $$
Commented by mathdanisur last updated on 09/Jul/21

$${thsnks}\:{Ser} \\ $$
Answered by mathmax by abdo last updated on 09/Jul/21
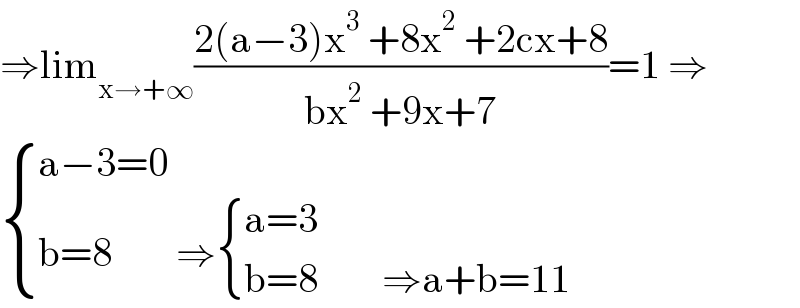
$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \frac{\mathrm{2}\left(\mathrm{a}−\mathrm{3}\right)\mathrm{x}^{\mathrm{3}} \:+\mathrm{8x}^{\mathrm{2}} \:+\mathrm{2cx}+\mathrm{8}}{\mathrm{bx}^{\mathrm{2}} \:+\mathrm{9x}+\mathrm{7}}=\mathrm{1}\:\Rightarrow \\ $$$$\begin{cases}{\mathrm{a}−\mathrm{3}=\mathrm{0}}\\{\mathrm{b}=\mathrm{8}\:\:\:\:\:\:\:\:\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{3}}\\{\mathrm{b}=\mathrm{8}\:\:\:\:\:\:\:\:\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{11}}\end{cases}}\end{cases} \\ $$
Commented by mathdanisur last updated on 09/Jul/21

$${thanks}\:{Ser} \\ $$
