Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 87175 by john santu last updated on 03/Apr/20

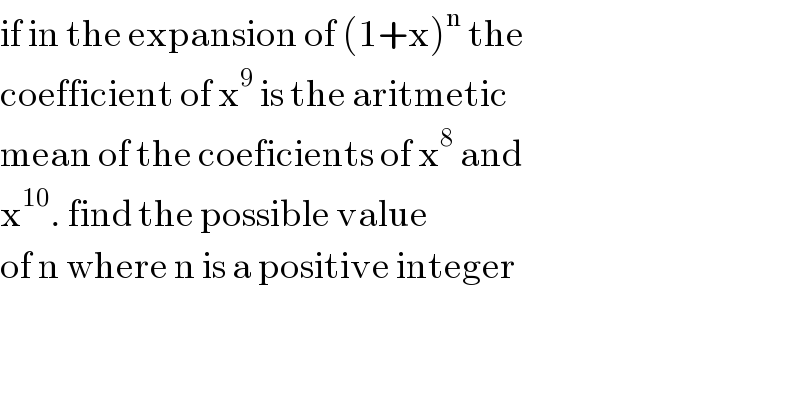
if in the expansion of (1+x)^n the coefficient of x^9 is the aritmetic mean of the coeficients of x^8 and x^(10) . find the possible value of n where n is a positive integer

$$\mathrm{if}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} \:\mathrm{the} \\ $$$$\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{9}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{aritmetic}\: \\ $$$$\mathrm{mean}\:\mathrm{of}\:\mathrm{the}\:\mathrm{coeficients}\:\mathrm{of}\:\mathrm{x}^{\mathrm{8}} \:\mathrm{and}\: \\ $$$$\mathrm{x}^{\mathrm{10}} .\:\mathrm{find}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{value}\: \\ $$$$\mathrm{of}\:\mathrm{n}\:\mathrm{where}\:\mathrm{n}\:\mathrm{is}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{integer} \\ $$

Commented by jagoll last updated on 03/Apr/20

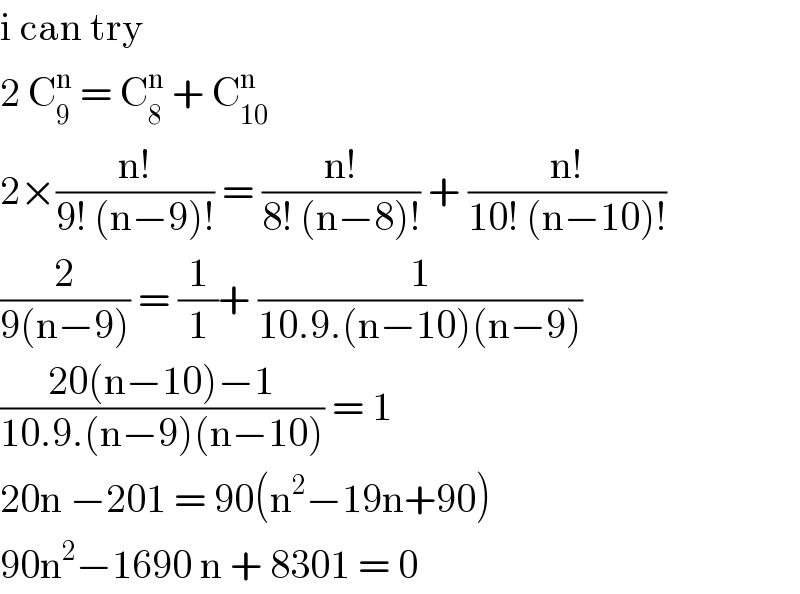
i can try 2 C_9 ^n = C_8 ^n + C_(10) ^n 2×((n!)/(9! (n−9)!)) = ((n!)/(8! (n−8)!)) + ((n!)/(10! (n−10)!)) (2/(9(n−9))) = (1/1)+ (1/(10.9.(n−10)(n−9))) ((20(n−10)−1)/(10.9.(n−9)(n−10))) = 1 20n −201 = 90(n^2 −19n+90) 90n^2 −1690 n + 8301 = 0

$$\mathrm{i}\:\mathrm{can}\:\mathrm{try}\: \\ $$$$\mathrm{2}\:\mathrm{C}_{\mathrm{9}} ^{\mathrm{n}} \:=\:\mathrm{C}_{\mathrm{8}} ^{\mathrm{n}} \:+\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{n}} \\ $$$$\mathrm{2}×\frac{\mathrm{n}!}{\mathrm{9}!\:\left(\mathrm{n}−\mathrm{9}\right)!}\:=\:\frac{\mathrm{n}!}{\mathrm{8}!\:\left(\mathrm{n}−\mathrm{8}\right)!}\:+\:\frac{\mathrm{n}!}{\mathrm{10}!\:\left(\mathrm{n}−\mathrm{10}\right)!} \\ $$$$\frac{\mathrm{2}}{\mathrm{9}\left(\mathrm{n}−\mathrm{9}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{1}}+\:\frac{\mathrm{1}}{\mathrm{10}.\mathrm{9}.\left(\mathrm{n}−\mathrm{10}\right)\left(\mathrm{n}−\mathrm{9}\right)} \\ $$$$\frac{\mathrm{20}\left(\mathrm{n}−\mathrm{10}\right)−\mathrm{1}}{\mathrm{10}.\mathrm{9}.\left(\mathrm{n}−\mathrm{9}\right)\left(\mathrm{n}−\mathrm{10}\right)}\:=\:\mathrm{1} \\ $$$$\mathrm{20n}\:−\mathrm{201}\:=\:\mathrm{90}\left(\mathrm{n}^{\mathrm{2}} −\mathrm{19n}+\mathrm{90}\right) \\ $$$$\mathrm{90n}^{\mathrm{2}} −\mathrm{1690}\:\mathrm{n}\:+\:\mathrm{8301}\:=\:\mathrm{0} \\ $$

Commented by john santu last updated on 03/Apr/20

good sir

$$\mathrm{good}\:\mathrm{sir} \\ $$

Answered by john santu last updated on 03/Apr/20

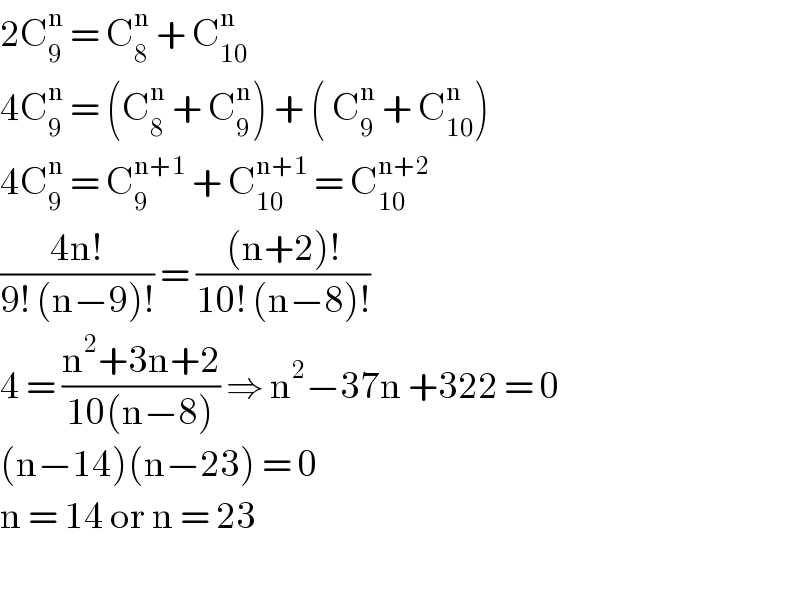
2C_9 ^n = C_8 ^n + C_(10) ^n 4C_9 ^n = (C_8 ^n + C_9 ^n ) + ( C_9 ^n + C_(10) ^n ) 4C_9 ^n = C_9 ^(n+1) + C_(10) ^(n+1) = C_(10) ^(n+2) ((4n!)/(9! (n−9)!)) = (((n+2)!)/(10! (n−8)!)) 4 = ((n^2 +3n+2)/(10(n−8))) ⇒ n^2 −37n +322 = 0 (n−14)(n−23) = 0 n = 14 or n = 23

$$\mathrm{2C}_{\mathrm{9}} ^{\mathrm{n}} \:=\:\mathrm{C}_{\mathrm{8}} ^{\mathrm{n}} \:+\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{n}} \\ $$$$\mathrm{4C}_{\mathrm{9}} ^{\mathrm{n}} \:=\:\left(\mathrm{C}_{\mathrm{8}} ^{\mathrm{n}} \:+\:\mathrm{C}_{\mathrm{9}} ^{\mathrm{n}} \right)\:+\:\left(\:\mathrm{C}_{\mathrm{9}} ^{\mathrm{n}} \:+\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{n}} \right)\: \\ $$$$\mathrm{4C}_{\mathrm{9}} ^{\mathrm{n}} \:=\:\mathrm{C}_{\mathrm{9}} ^{\mathrm{n}+\mathrm{1}} \:+\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{n}+\mathrm{1}} \:=\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{n}+\mathrm{2}} \\ $$$$\frac{\mathrm{4n}!}{\mathrm{9}!\:\left(\mathrm{n}−\mathrm{9}\right)!}\:=\:\frac{\left(\mathrm{n}+\mathrm{2}\right)!}{\mathrm{10}!\:\left(\mathrm{n}−\mathrm{8}\right)!} \\ $$$$\mathrm{4}\:=\:\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{2}}{\mathrm{10}\left(\mathrm{n}−\mathrm{8}\right)}\:\Rightarrow\:\mathrm{n}^{\mathrm{2}} −\mathrm{37n}\:+\mathrm{322}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{n}−\mathrm{14}\right)\left(\mathrm{n}−\mathrm{23}\right)\:=\:\mathrm{0}\: \\ $$$$\mathrm{n}\:=\:\mathrm{14}\:\mathrm{or}\:\mathrm{n}\:=\:\mathrm{23}\: \\ $$$$ \\ $$

Commented by peter frank last updated on 03/Apr/20

good

$${good}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com