
Question Number 206458 by mathlove last updated on 15/Apr/24
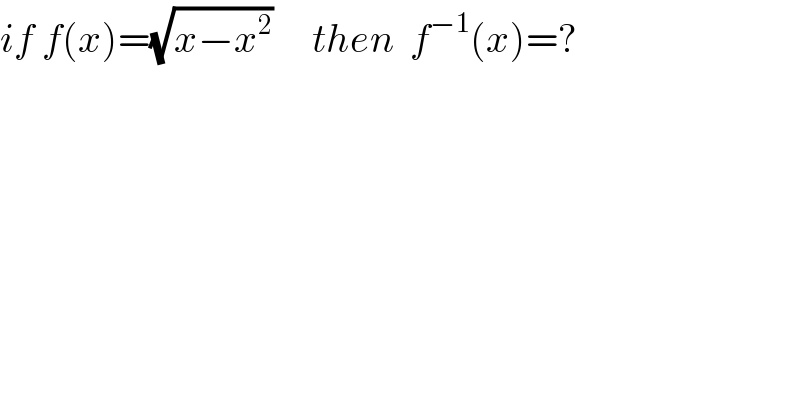
$${if}\:{f}\left({x}\right)=\sqrt{{x}−{x}^{\mathrm{2}} }\:\:\:\:\:{then}\:\:{f}^{−\mathrm{1}} \left({x}\right)=? \\ $$
Answered by Skabetix last updated on 15/Apr/24
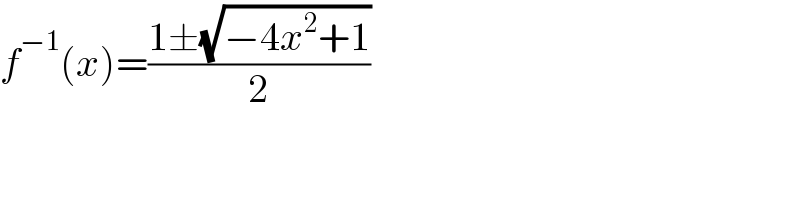
$${f}^{−\mathrm{1}} \left({x}\right)=\frac{\mathrm{1}\pm\sqrt{−\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}} \\ $$
Commented by Tinku Tara last updated on 15/Apr/24
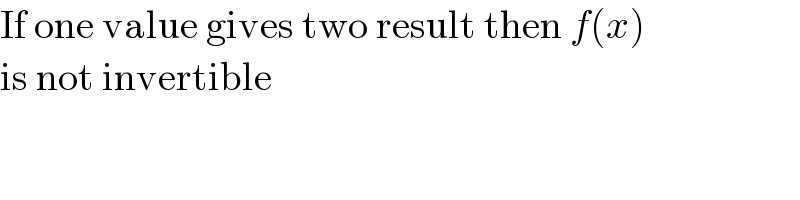
$$\mathrm{If}\:\mathrm{one}\:\mathrm{value}\:\mathrm{gives}\:\mathrm{two}\:\mathrm{result}\:\mathrm{then}\:{f}\left({x}\right) \\ $$$$\mathrm{is}\:\mathrm{not}\:\mathrm{invertible} \\ $$
Commented by mathlove last updated on 15/Apr/24

$${yes}\:{sir} \\ $$
Answered by cortano21 last updated on 15/Apr/24

$$\:\:\:\: \\ $$
Answered by Frix last updated on 15/Apr/24
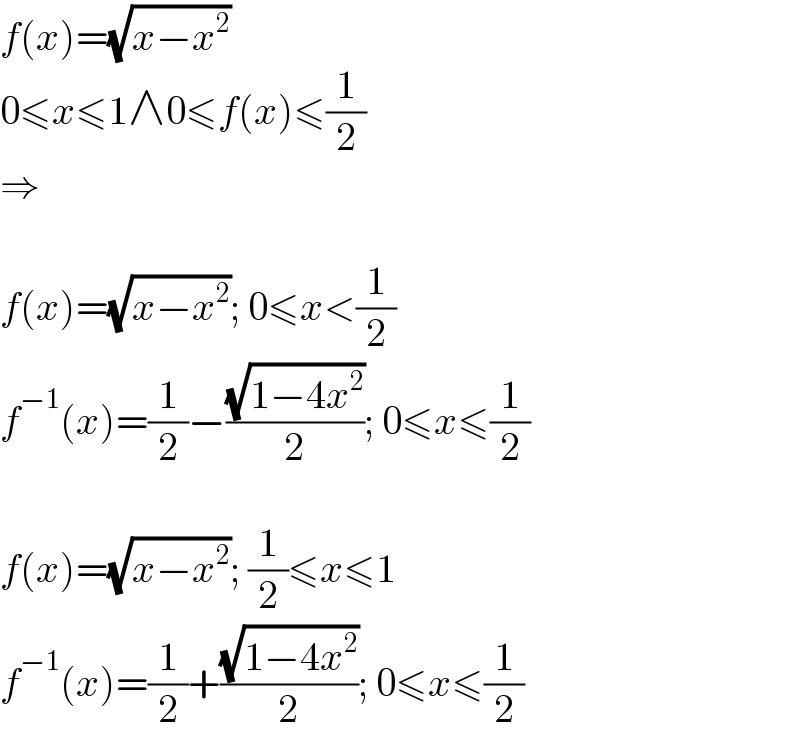
$${f}\left({x}\right)=\sqrt{{x}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\wedge\mathrm{0}\leqslant{f}\left({x}\right)\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$ \\ $$$${f}\left({x}\right)=\sqrt{{x}−{x}^{\mathrm{2}} };\:\mathrm{0}\leqslant{x}<\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{2}};\:\mathrm{0}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${f}\left({x}\right)=\sqrt{{x}−{x}^{\mathrm{2}} };\:\frac{\mathrm{1}}{\mathrm{2}}\leqslant{x}\leqslant\mathrm{1} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{2}};\:\mathrm{0}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$
