Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 66412 by aliesam last updated on 14/Aug/19

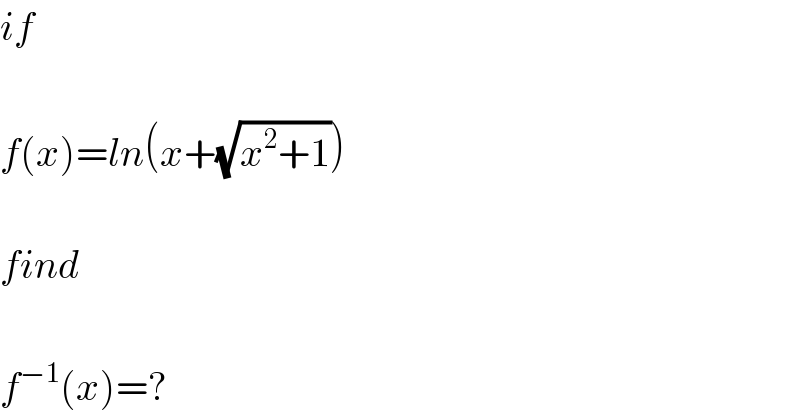
if f(x)=ln(x+(√(x^2 +1))) find f^(−1) (x)=?

$${if} \\ $$$$ \\ $$$${f}\left({x}\right)={ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$ \\ $$$${find} \\ $$$$ \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=? \\ $$

Commented by mathmax by abdo last updated on 14/Aug/19

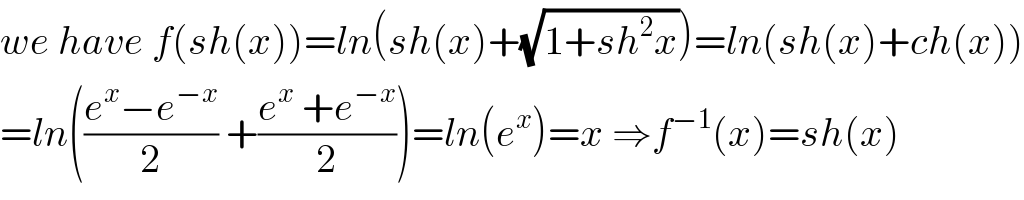
we have f(sh(x))=ln(sh(x)+(√(1+sh^2 x)))=ln(sh(x)+ch(x)) =ln(((e^x −e^(−x) )/2) +((e^x +e^(−x) )/2))=ln(e^x )=x ⇒f^(−1) (x)=sh(x)

$${we}\:{have}\:{f}\left({sh}\left({x}\right)\right)={ln}\left({sh}\left({x}\right)+\sqrt{\mathrm{1}+{sh}^{\mathrm{2}} {x}}\right)={ln}\left({sh}\left({x}\right)+{ch}\left({x}\right)\right) \\ $$$$={ln}\left(\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}}\:+\frac{{e}^{{x}} \:+{e}^{−{x}} }{\mathrm{2}}\right)={ln}\left({e}^{{x}} \right)={x}\:\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)={sh}\left({x}\right) \\ $$

Commented by mr W last updated on 14/Aug/19

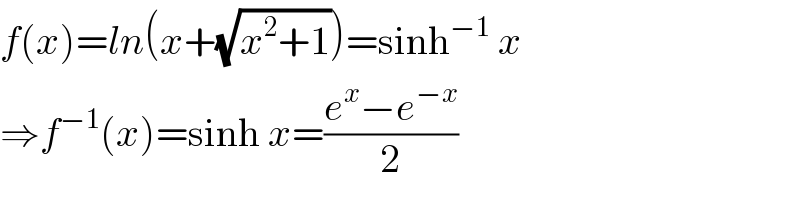
f(x)=ln(x+(√(x^2 +1)))=sinh^(−1) x ⇒f^(−1) (x)=sinh x=((e^x −e^(−x) )/2)

$${f}\left({x}\right)={ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)=\mathrm{sinh}^{−\mathrm{1}} \:{x} \\ $$$$\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\mathrm{sinh}\:{x}=\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}} \\ $$

Commented by kaivan.ahmadi last updated on 15/Aug/19

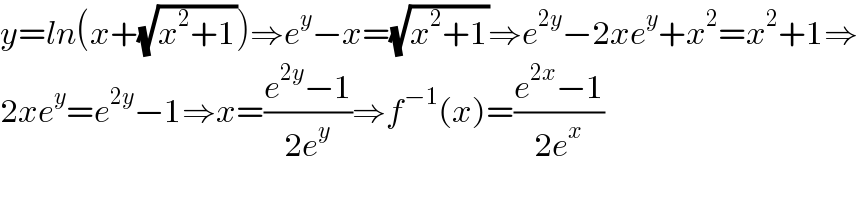
y=ln(x+(√(x^2 +1)))⇒e^y −x=(√(x^2 +1))⇒e^(2y) −2xe^y +x^2 =x^2 +1⇒ 2xe^y =e^(2y) −1⇒x=((e^(2y) −1)/(2e^y ))⇒f^(−1) (x)=((e^(2x) −1)/(2e^x ))

$${y}={ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\Rightarrow{e}^{{y}} −{x}=\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\Rightarrow{e}^{\mathrm{2}{y}} −\mathrm{2}{xe}^{{y}} +{x}^{\mathrm{2}} ={x}^{\mathrm{2}} +\mathrm{1}\Rightarrow \\ $$$$\mathrm{2}{xe}^{{y}} ={e}^{\mathrm{2}{y}} −\mathrm{1}\Rightarrow{x}=\frac{{e}^{\mathrm{2}{y}} −\mathrm{1}}{\mathrm{2}{e}^{{y}} }\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{\mathrm{2}{e}^{{x}} } \\ $$

Answered by MJS last updated on 14/Aug/19

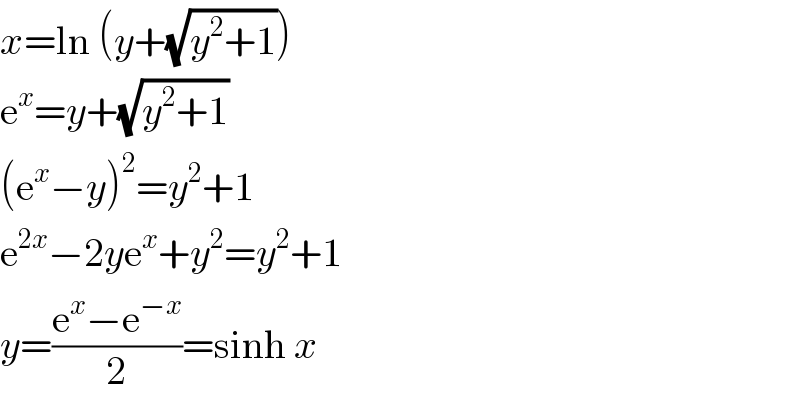
x=ln (y+(√(y^2 +1))) e^x =y+(√(y^2 +1)) (e^x −y)^2 =y^2 +1 e^(2x) −2ye^x +y^2 =y^2 +1 y=((e^x −e^(−x) )/2)=sinh x

$${x}=\mathrm{ln}\:\left({y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$\mathrm{e}^{{x}} ={y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\left(\mathrm{e}^{{x}} −{y}\right)^{\mathrm{2}} ={y}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{e}^{\mathrm{2}{x}} −\mathrm{2}{y}\mathrm{e}^{{x}} +{y}^{\mathrm{2}} ={y}^{\mathrm{2}} +\mathrm{1} \\ $$$${y}=\frac{\mathrm{e}^{{x}} −\mathrm{e}^{−{x}} }{\mathrm{2}}=\mathrm{sinh}\:{x} \\ $$

Commented by Mikael last updated on 15/Aug/19

nice Sir.

$${nice}\:{Sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com