
Question Number 543 by 123456 last updated on 25/Jan/15
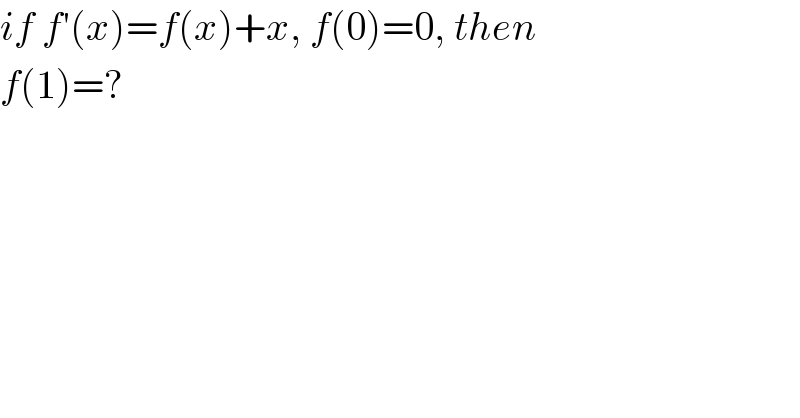
$${if}\:{f}'\left({x}\right)={f}\left({x}\right)+{x},\:{f}\left(\mathrm{0}\right)=\mathrm{0},\:{then} \\ $$$${f}\left(\mathrm{1}\right)=? \\ $$
Answered by prakash jain last updated on 24/Jan/15
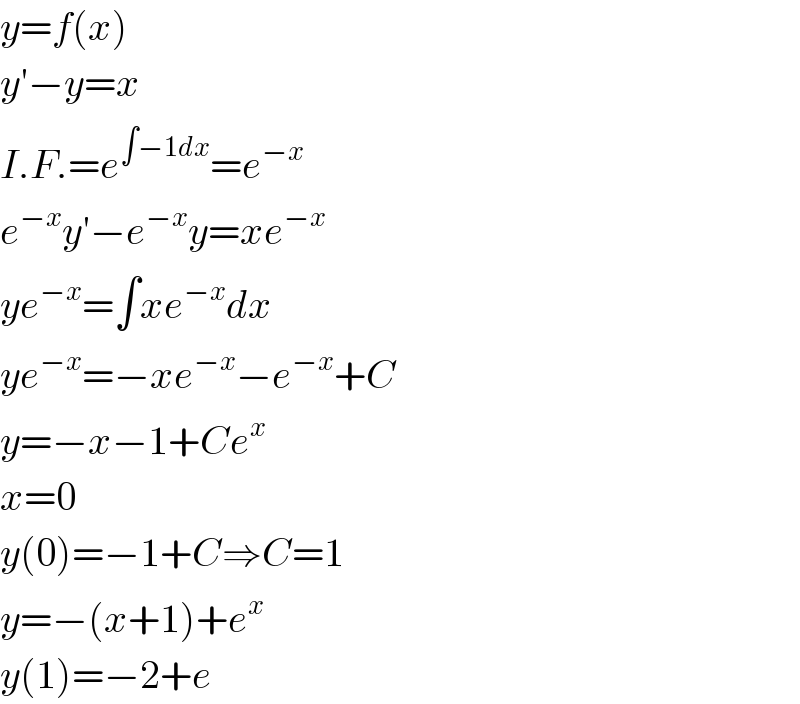
$${y}={f}\left({x}\right) \\ $$$${y}'−{y}={x} \\ $$$${I}.{F}.={e}^{\int−\mathrm{1}{dx}} ={e}^{−{x}} \\ $$$${e}^{−{x}} {y}'−{e}^{−{x}} {y}={xe}^{−{x}} \\ $$$${ye}^{−{x}} =\int{xe}^{−{x}} {dx} \\ $$$${ye}^{−{x}} =−{xe}^{−{x}} −{e}^{−{x}} +{C} \\ $$$${y}=−{x}−\mathrm{1}+{Ce}^{{x}} \\ $$$${x}=\mathrm{0} \\ $$$${y}\left(\mathrm{0}\right)=−\mathrm{1}+{C}\Rightarrow{C}=\mathrm{1} \\ $$$${y}=−\left({x}+\mathrm{1}\right)+{e}^{{x}} \\ $$$${y}\left(\mathrm{1}\right)=−\mathrm{2}+{e} \\ $$
