
Question Number 113854 by ayenisamuel last updated on 15/Sep/20
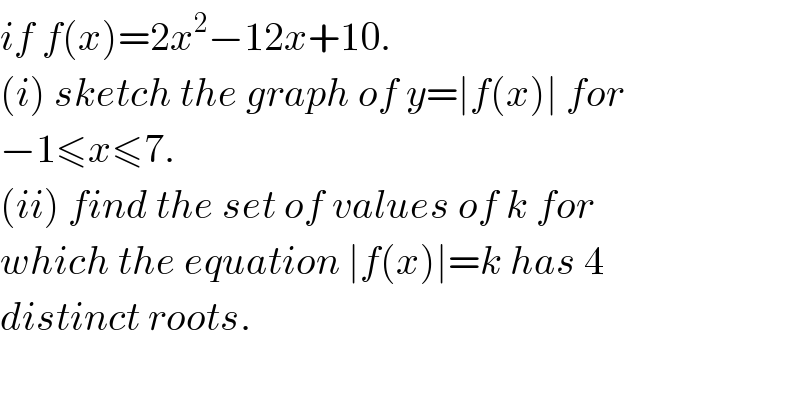
$${if}\:{f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{10}.\: \\ $$$$\left({i}\right)\:{sketch}\:{the}\:{graph}\:{of}\:{y}=\mid{f}\left({x}\right)\mid\:{for} \\ $$$$−\mathrm{1}\leqslant{x}\leqslant\mathrm{7}. \\ $$$$\left({ii}\right)\:{find}\:{the}\:{set}\:{of}\:{values}\:{of}\:{k}\:{for} \\ $$$${which}\:{the}\:{equation}\:\mid{f}\left({x}\right)\mid={k}\:{has}\:\mathrm{4} \\ $$$${distinct}\:{roots}. \\ $$
Answered by MJS_new last updated on 15/Sep/20
![∣2x^2 −12x+10∣=k ⇒ k≥0 (2x^2 −12x+10)^2 =k^2 x^4 −12x^3 +46x^2 −60x−(k^2 /4)+25=0 let x=t+3 t^4 −8t^2 −(k^2 /4)+16=0 ⇒ t^2 =((8±k)/2) ⇒ t=±(√((8±k)/2)) [4 solutions] ⇒ x_(1, 2) =3±(√((8−k)/2)); x_(3, 4) =3±(√((8+k)/2)) ⇒ 4 solutions only if 8−k>0∧8+k>0 ⇒ −8<k<8 but k≥0 ⇒ 0≤k<8](Q113864.png)
$$\mid\mathrm{2}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{10}\mid={k}\:\Rightarrow\:{k}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{10}\right)^{\mathrm{2}} ={k}^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} −\mathrm{12}{x}^{\mathrm{3}} +\mathrm{46}{x}^{\mathrm{2}} −\mathrm{60}{x}−\frac{{k}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{25}=\mathrm{0} \\ $$$$\mathrm{let}\:{x}={t}+\mathrm{3} \\ $$$${t}^{\mathrm{4}} −\mathrm{8}{t}^{\mathrm{2}} −\frac{{k}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow\:{t}^{\mathrm{2}} =\frac{\mathrm{8}\pm{k}}{\mathrm{2}}\:\Rightarrow\:{t}=\pm\sqrt{\frac{\mathrm{8}\pm{k}}{\mathrm{2}}}\:\:\:\left[\mathrm{4}\:\mathrm{solutions}\right] \\ $$$$\Rightarrow\:{x}_{\mathrm{1},\:\mathrm{2}} =\mathrm{3}\pm\sqrt{\frac{\mathrm{8}−{k}}{\mathrm{2}}};\:{x}_{\mathrm{3},\:\mathrm{4}} =\mathrm{3}\pm\sqrt{\frac{\mathrm{8}+{k}}{\mathrm{2}}} \\ $$$$\Rightarrow\:\mathrm{4}\:\mathrm{solutions}\:\mathrm{only}\:\mathrm{if}\:\mathrm{8}−{k}>\mathrm{0}\wedge\mathrm{8}+{k}>\mathrm{0} \\ $$$$\Rightarrow\:−\mathrm{8}<{k}<\mathrm{8}\:\mathrm{but}\:{k}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{0}\leqslant{k}<\mathrm{8} \\ $$
