
Question Number 201464 by hardmath last updated on 06/Dec/23
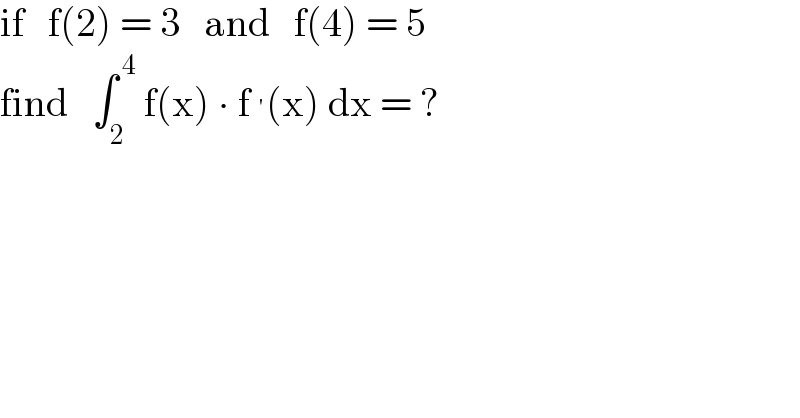
$$\mathrm{if}\:\:\:\mathrm{f}\left(\mathrm{2}\right)\:=\:\mathrm{3}\:\:\:\mathrm{and}\:\:\:\mathrm{f}\left(\mathrm{4}\right)\:=\:\mathrm{5} \\ $$$$\mathrm{find}\:\:\:\int_{\mathrm{2}} ^{\:\mathrm{4}} \:\mathrm{f}\left(\mathrm{x}\right)\:\centerdot\:\mathrm{f}\:^{'} \left(\mathrm{x}\right)\:\mathrm{dx}\:=\:? \\ $$
Answered by mahdipoor last updated on 06/Dec/23
![=[(((f(x))^2 )/2)]_2 ^4 =((25−9)/2)=8](Q201466.png)
$$=\left[\frac{\left({f}\left({x}\right)\right)^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{2}} ^{\mathrm{4}} =\frac{\mathrm{25}−\mathrm{9}}{\mathrm{2}}=\mathrm{8} \\ $$
Commented by hardmath last updated on 06/Dec/23

$$\mathrm{thank}\:\mathrm{you},\:\mathrm{but}\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{understand} \\ $$
Answered by mr W last updated on 07/Dec/23
![let u=f(x) du=f′(x)dx at x=2: u=f(2)=3 at x=4: u=f4)=5 ∫_2 ^4 f(x)f′(x)dx =∫_(f(2)) ^(f(4)) udu =[(u^2 /2)]_(f(2)) ^(f(4)) =[(u^2 /2)]_3 ^5 =((5^2 −3^2 )/2) =8](Q201470.png)
$${let}\:{u}={f}\left({x}\right) \\ $$$${du}={f}'\left({x}\right){dx} \\ $$$${at}\:{x}=\mathrm{2}:\:{u}={f}\left(\mathrm{2}\right)=\mathrm{3} \\ $$$$\left.{at}\:{x}=\mathrm{4}:\:{u}={f}\mathrm{4}\right)=\mathrm{5} \\ $$$$\int_{\mathrm{2}} ^{\mathrm{4}} {f}\left({x}\right){f}'\left({x}\right){dx} \\ $$$$=\int_{{f}\left(\mathrm{2}\right)} ^{{f}\left(\mathrm{4}\right)} {udu} \\ $$$$=\left[\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right]_{{f}\left(\mathrm{2}\right)} ^{{f}\left(\mathrm{4}\right)} \\ $$$$=\left[\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{3}} ^{\mathrm{5}} \\ $$$$=\frac{\mathrm{5}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\mathrm{8} \\ $$
Commented by Calculusboy last updated on 06/Dec/23

$$\boldsymbol{{nice}}\:\boldsymbol{{solution}} \\ $$
Commented by hardmath last updated on 08/Dec/23
$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
