
Question Number 63399 by smartsmith459@gmail.com last updated on 03/Jul/19
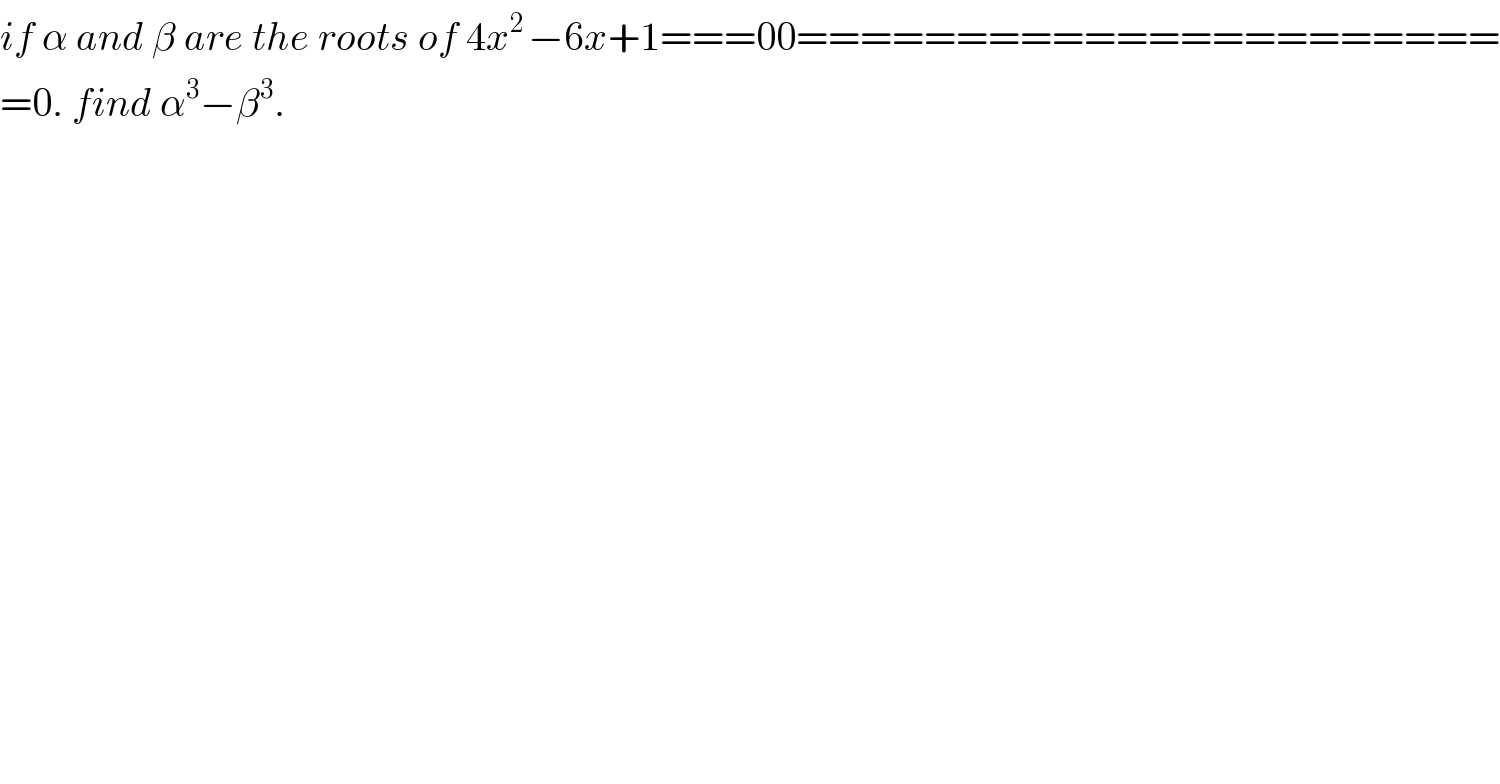
$${if}\:\alpha\:{and}\:\beta\:{are}\:{the}\:{roots}\:{of}\:\mathrm{4}{x}^{\mathrm{2}\:} −\mathrm{6}{x}+\mathrm{1}===\mathrm{00}====================== \\ $$$$=\mathrm{0}.\:{find}\:\alpha^{\mathrm{3}} −\beta^{\mathrm{3}} . \\ $$
Commented by mr W last updated on 03/Jul/19
![α+β=(6/4)=(3/2) αβ=(1/4) (α−β)^2 =(α+β)^2 −4αβ ⇒(α−β)=±(√((α+β)^2 −4αβ)) α^3 −β^3 =(α−β)(α^2 +β^2 +αβ) =(α−β)[(α+β)^2 −αβ] =±(√((α+β)^2 −4αβ))[(α+β)^2 −αβ] =±(√((9/4)−1))[(9/4)−(1/4)] =±2(√(5/4)) =±(√5)](Q63413.png)
$$\alpha+\beta=\frac{\mathrm{6}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\alpha\beta=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$$\left(\alpha−\beta\right)^{\mathrm{2}} =\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{4}\alpha\beta \\ $$$$\Rightarrow\left(\alpha−\beta\right)=\pm\sqrt{\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{4}\alpha\beta} \\ $$$$ \\ $$$$\alpha^{\mathrm{3}} −\beta^{\mathrm{3}} \\ $$$$=\left(\alpha−\beta\right)\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\alpha\beta\right) \\ $$$$=\left(\alpha−\beta\right)\left[\left(\alpha+\beta\right)^{\mathrm{2}} −\alpha\beta\right] \\ $$$$=\pm\sqrt{\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{4}\alpha\beta}\left[\left(\alpha+\beta\right)^{\mathrm{2}} −\alpha\beta\right] \\ $$$$=\pm\sqrt{\frac{\mathrm{9}}{\mathrm{4}}−\mathrm{1}}\left[\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\right] \\ $$$$=\pm\mathrm{2}\sqrt{\frac{\mathrm{5}}{\mathrm{4}}} \\ $$$$=\pm\sqrt{\mathrm{5}} \\ $$
Answered by MJS last updated on 03/Jul/19
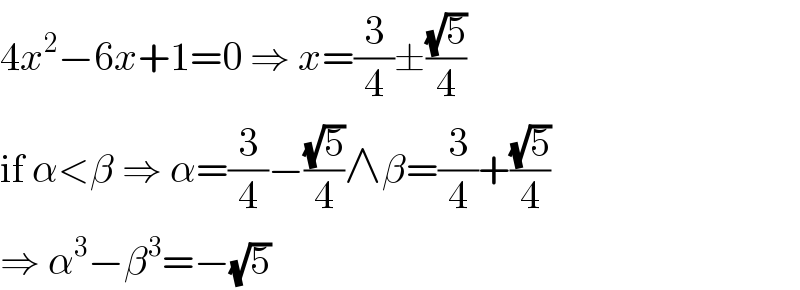
$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:{x}=\frac{\mathrm{3}}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{if}\:\alpha<\beta\:\Rightarrow\:\alpha=\frac{\mathrm{3}}{\mathrm{4}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}\wedge\beta=\frac{\mathrm{3}}{\mathrm{4}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\Rightarrow\:\alpha^{\mathrm{3}} −\beta^{\mathrm{3}} =−\sqrt{\mathrm{5}} \\ $$
