Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 211421 by universe last updated on 08/Sep/24

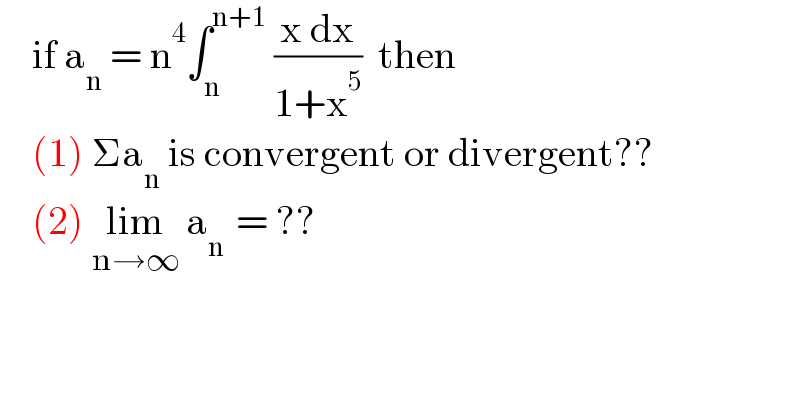
if a_n = n^4 ∫_n ^(n+1) ((x dx)/(1+x^5 )) then (1) Σa_n is convergent or divergent?? (2) lim_(n→∞) a_(n ) = ??

$$\:\:\:\:\mathrm{if}\:\mathrm{a}_{\mathrm{n}} \:=\:\mathrm{n}^{\mathrm{4}} \int_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{x}\:\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{5}} }\:\:\mathrm{then} \\ $$$$\:\:\:\:\left(\mathrm{1}\right)\:\Sigma\mathrm{a}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{convergent}\:\mathrm{or}\:\mathrm{divergent}?? \\ $$$$\:\:\:\:\left(\mathrm{2}\right)\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{a}_{\mathrm{n}\:} \:=\:?? \\ $$

Answered by mathmax last updated on 09/Sep/24

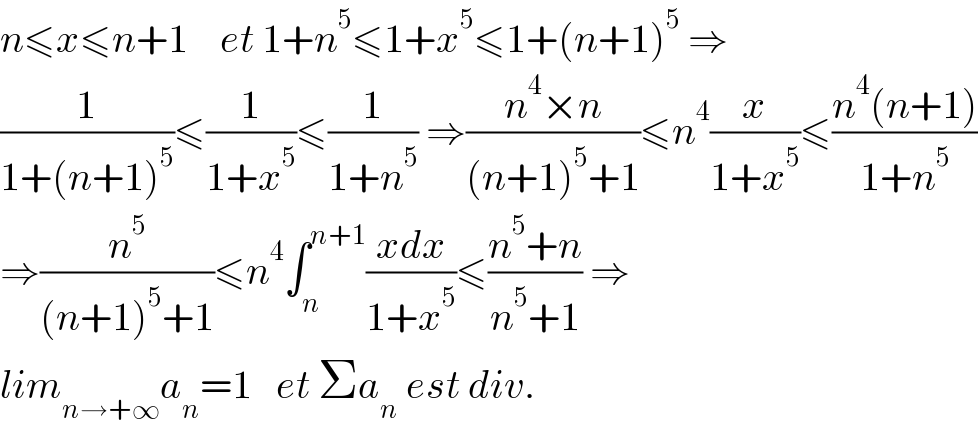
n≤x≤n+1 et 1+n^5 ≤1+x^5 ≤1+(n+1)^5 ⇒ (1/(1+(n+1)^5 ))≤(1/(1+x^5 ))≤(1/(1+n^5 )) ⇒((n^4 ×n)/((n+1)^5 +1))≤n^4 (x/(1+x^5 ))≤((n^4 (n+1))/(1+n^5 )) ⇒(n^5 /((n+1)^5 +1))≤n^4 ∫_n ^(n+1) ((xdx)/(1+x^5 ))≤((n^5 +n)/(n^5 +1)) ⇒ lim_(n→+∞) a_n =1 et Σa_n est div.

$${n}\leqslant{x}\leqslant{n}+\mathrm{1}\:\:\:\:{et}\:\mathrm{1}+{n}^{\mathrm{5}} \leqslant\mathrm{1}+{x}^{\mathrm{5}} \leqslant\mathrm{1}+\left({n}+\mathrm{1}\right)^{\mathrm{5}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\left({n}+\mathrm{1}\right)^{\mathrm{5}} }\leqslant\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{5}} }\leqslant\frac{\mathrm{1}}{\mathrm{1}+{n}^{\mathrm{5}} }\:\Rightarrow\frac{{n}^{\mathrm{4}} ×{n}}{\left({n}+\mathrm{1}\right)^{\mathrm{5}} +\mathrm{1}}\leqslant{n}^{\mathrm{4}} \frac{{x}}{\mathrm{1}+{x}^{\mathrm{5}} }\leqslant\frac{{n}^{\mathrm{4}} \left({n}+\mathrm{1}\right)}{\mathrm{1}+{n}^{\mathrm{5}} } \\ $$$$\Rightarrow\frac{{n}^{\mathrm{5}} }{\left({n}+\mathrm{1}\right)^{\mathrm{5}} +\mathrm{1}}\leqslant{n}^{\mathrm{4}} \int_{{n}} ^{{n}+\mathrm{1}} \frac{{xdx}}{\mathrm{1}+{x}^{\mathrm{5}} }\leqslant\frac{{n}^{\mathrm{5}} +{n}}{{n}^{\mathrm{5}} +\mathrm{1}}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} {a}_{{n}} =\mathrm{1}\:\:\:{et}\:\Sigma{a}_{{n}} \:{est}\:{div}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com