
Question Number 192009 by universe last updated on 05/May/23
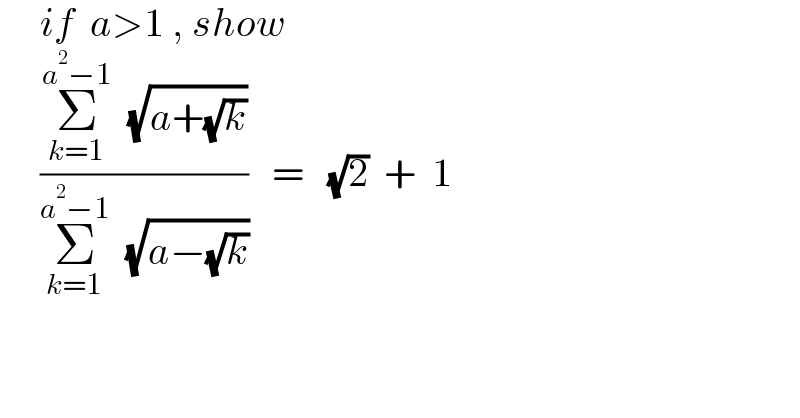
$$\:\:\:\:\:{if}\:\:{a}>\mathrm{1}\:,\:{show} \\ $$$$\:\:\:\:\:\frac{\underset{{k}=\mathrm{1}} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}\:\:\sqrt{{a}+\sqrt{{k}}}}{\underset{{k}=\mathrm{1}} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}\:\:\sqrt{{a}−\sqrt{{k}}}}\:\:\:=\:\:\:\sqrt{\mathrm{2}}\:\:+\:\:\mathrm{1} \\ $$
Answered by Skabetix last updated on 05/May/23

Commented by Skabetix last updated on 05/May/23
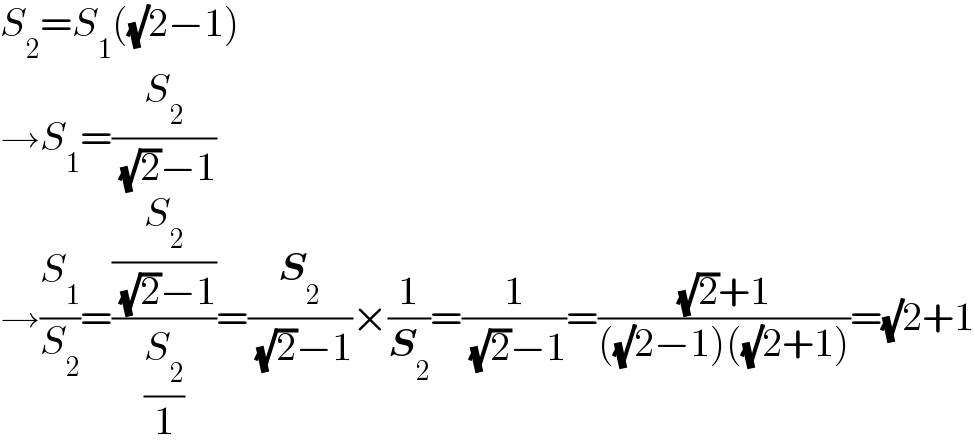
$${S}_{\mathrm{2}} ={S}_{\mathrm{1}} \left(\sqrt{}\mathrm{2}−\mathrm{1}\right) \\ $$$$\rightarrow{S}_{\mathrm{1}} =\frac{{S}_{\mathrm{2}} }{\:\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$\rightarrow\frac{{S}_{\mathrm{1}} }{{S}_{\mathrm{2}} }=\frac{\frac{{S}_{\mathrm{2}} }{\:\sqrt{\mathrm{2}}−\mathrm{1}}}{\frac{{S}_{\mathrm{2}} }{\mathrm{1}}}=\frac{\boldsymbol{{S}}_{\mathrm{2}} }{\:\sqrt{\mathrm{2}}−\mathrm{1}}×\frac{\mathrm{1}}{\boldsymbol{{S}}_{\mathrm{2}} }=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}=\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\left(\sqrt{}\mathrm{2}−\mathrm{1}\right)\left(\sqrt{}\mathrm{2}+\mathrm{1}\right)}=\sqrt{}\mathrm{2}+\mathrm{1} \\ $$
Answered by York12 last updated on 24/Jul/23
![let Σ_(k=1 ) ^(a^2 −1) (√(a+(√k) ))=s_1 and Σ_(k=1) ^(a^2 −1) (√(a−(√k)))=s_2 s_1 −s_2 =Σ_(k=1) ^(a^2 −1) [(√(((√(a+(√k)))−(√(a−(√k))))^2 ))]=Σ_(k=1) ^(a^2 −1) (√2)(√(a−(√(a^2 −k)))) → [I] Now since Σ_(k=1) ^(a^2 −1) T_k =Σ_(k=1) ^(a^2 −1) T_([(a^2 −1)−(k−1)]) =Σ_(k=1) ^(a^2 −1) T_((a^2 −k)) let T_k =(√(a−(√k) )) → T_((a^2 −k)) =(√(a−(√(a^2 −k)))) ∴ I = Σ_(k=1) ^(a^2 −1) (√(a−(√k)))=(√2)s_2 ∴ s_1 +s_2 =(√2)s_2 → s_1 =(1+(√2))s_2 → (s_1 /s_2 )=(1+(√2)) → (That′s it )](Q192070.png)
$${let}\:\underset{{k}=\mathrm{1}\:} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{a}+\sqrt{{k}}\:}={s}_{\mathrm{1}} \:\:{and}\:\underset{{k}=\mathrm{1}} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{a}−\sqrt{{k}}}={s}_{\mathrm{2}} \\ $$$${s}_{\mathrm{1}} −{s}_{\mathrm{2}} =\underset{{k}=\mathrm{1}} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}\left[\sqrt{\left(\sqrt{{a}+\sqrt{{k}}}−\sqrt{{a}−\sqrt{{k}}}\right)^{\mathrm{2}} }\right]=\underset{{k}=\mathrm{1}} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{\mathrm{2}}\sqrt{{a}−\sqrt{{a}^{\mathrm{2}} −{k}}}\:\:\:\:\:\rightarrow\:\left[\boldsymbol{{I}}\right] \\ $$$${Now}\:{since}\:\underset{{k}=\mathrm{1}} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}{T}_{{k}} =\underset{{k}=\mathrm{1}} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}{T}_{\left[\left({a}^{\mathrm{2}} −\mathrm{1}\right)−\left({k}−\mathrm{1}\right)\right]} =\underset{{k}=\mathrm{1}} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}{T}_{\left({a}^{\mathrm{2}} −{k}\right)} \\ $$$${let}\:{T}_{{k}} =\sqrt{{a}−\sqrt{{k}}\:}\:\rightarrow\:{T}_{\left({a}^{\mathrm{2}} −{k}\right)} =\sqrt{{a}−\sqrt{{a}^{\mathrm{2}} −{k}}} \\ $$$$\therefore\:\boldsymbol{{I}}\:=\:\underset{{k}=\mathrm{1}} {\overset{{a}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{a}−\sqrt{{k}}}=\sqrt{\mathrm{2}}{s}_{\mathrm{2}} \\ $$$$\therefore\:{s}_{\mathrm{1}} +{s}_{\mathrm{2}} =\sqrt{\mathrm{2}}{s}_{\mathrm{2}} \:\rightarrow\:{s}_{\mathrm{1}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){s}_{\mathrm{2}} \:\rightarrow\:\frac{{s}_{\mathrm{1}} }{{s}_{\mathrm{2}} }=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\rightarrow\:\left({That}'{s}\:{it}\:\right)\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
