Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 89991 by jagoll last updated on 20/Apr/20

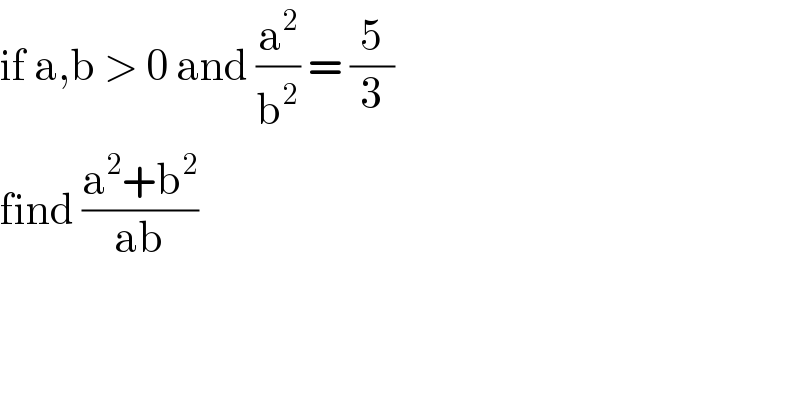
if a,b > 0 and (a^2 /b^2 ) = (5/3) find ((a^2 +b^2 )/(ab))

$$\mathrm{if}\:\mathrm{a},\mathrm{b}\:>\:\mathrm{0}\:\mathrm{and}\:\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} }\:=\:\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{find}\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{ab}} \\ $$

Commented by john santu last updated on 20/Apr/20

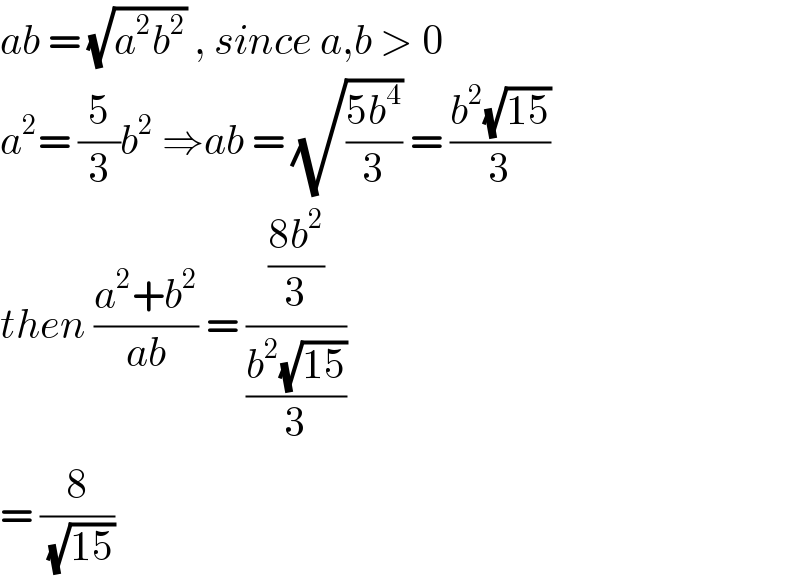
ab = (√(a^2 b^2 )) , since a,b > 0 a^2 = (5/3)b^2 ⇒ab = (√((5b^4 )/3)) = ((b^2 (√(15)))/3) then ((a^2 +b^2 )/(ab)) = (((8b^2 )/3)/((b^2 (√(15)))/3)) = (8/(√(15)))

$${ab}\:=\:\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\:,\:{since}\:{a},{b}\:>\:\mathrm{0} \\ $$$${a}^{\mathrm{2}} =\:\frac{\mathrm{5}}{\mathrm{3}}{b}^{\mathrm{2}} \:\Rightarrow{ab}\:=\:\sqrt{\frac{\mathrm{5}{b}^{\mathrm{4}} }{\mathrm{3}}}\:=\:\frac{{b}^{\mathrm{2}} \sqrt{\mathrm{15}}}{\mathrm{3}} \\ $$$${then}\:\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{ab}}\:=\:\frac{\frac{\mathrm{8}{b}^{\mathrm{2}} }{\mathrm{3}}}{\frac{{b}^{\mathrm{2}} \sqrt{\mathrm{15}}}{\mathrm{3}}} \\ $$$$=\:\frac{\mathrm{8}}{\sqrt{\mathrm{15}}} \\ $$

Commented by mr W last updated on 20/Apr/20

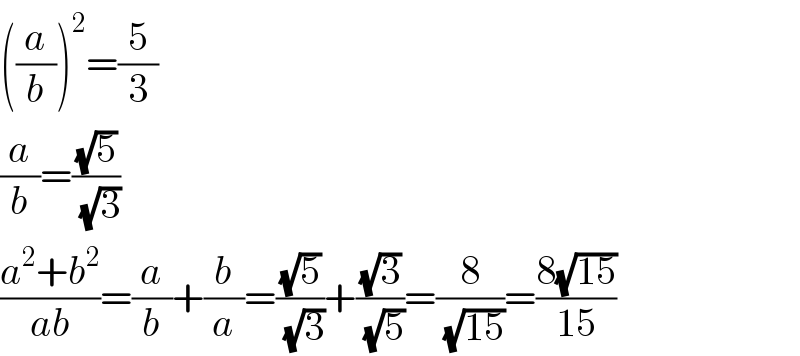
((a/b))^2 =(5/3) (a/b)=((√5)/(√3)) ((a^2 +b^2 )/(ab))=(a/b)+(b/a)=((√5)/(√3))+((√3)/(√5))=(8/(√(15)))=((8(√(15)))/(15))

$$\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\frac{{a}}{{b}}=\frac{\sqrt{\mathrm{5}}}{\sqrt{\mathrm{3}}} \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{ab}}=\frac{{a}}{{b}}+\frac{{b}}{{a}}=\frac{\sqrt{\mathrm{5}}}{\sqrt{\mathrm{3}}}+\frac{\sqrt{\mathrm{3}}}{\sqrt{\mathrm{5}}}=\frac{\mathrm{8}}{\sqrt{\mathrm{15}}}=\frac{\mathrm{8}\sqrt{\mathrm{15}}}{\mathrm{15}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com