
Question Number 217140 by peter frank last updated on 02/Mar/25

if a, b, c are three digits, abc and bca are two numbers. where abc +cba = 444, b =2. find the value of a+b+c.
Answered by Rasheed.Sindhi last updated on 02/Mar/25
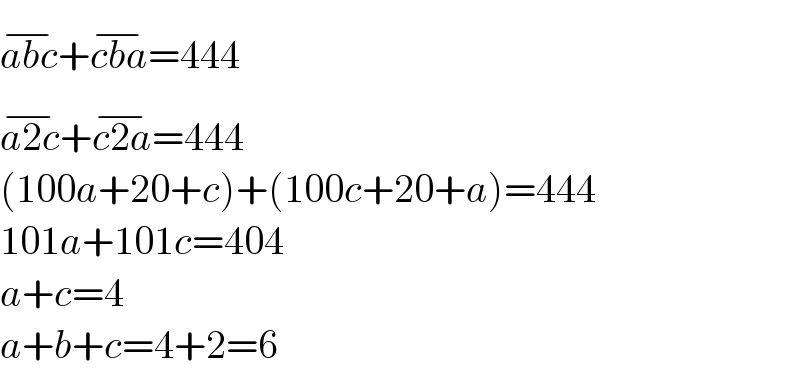
$$\overline {{abc}}+\overline {{cba}}=\mathrm{444} \\ $$$$\overline {{a}\mathrm{2}{c}}+\overline {{c}\mathrm{2}{a}}=\mathrm{444} \\ $$$$\left(\mathrm{100}{a}+\mathrm{20}+{c}\right)+\left(\mathrm{100}{c}+\mathrm{20}+{a}\right)=\mathrm{444} \\ $$$$\mathrm{101}{a}+\mathrm{101}{c}=\mathrm{404} \\ $$$${a}+{c}=\mathrm{4} \\ $$$${a}+{b}+{c}=\mathrm{4}+\mathrm{2}=\mathrm{6} \\ $$
Commented by peter frank last updated on 02/Mar/25

$$\mathrm{thank}\:\:\mathrm{you} \\ $$
