Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 193546 by York12 last updated on 16/Jun/23

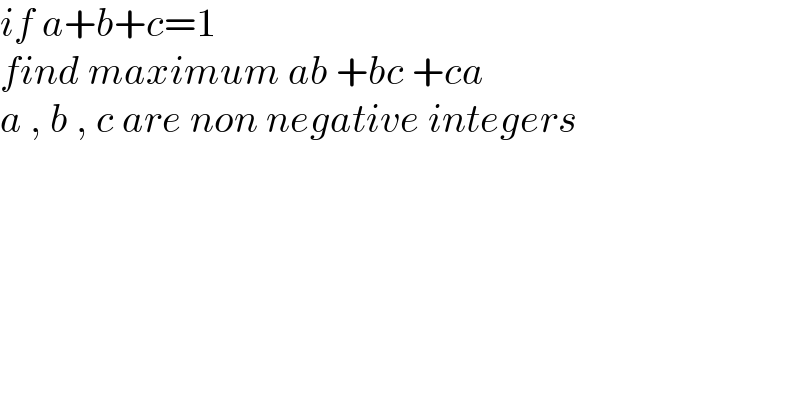
if a+b+c=1 find maximum ab +bc +ca a , b , c are non negative integers

$${if}\:{a}+{b}+{c}=\mathrm{1} \\ $$$${find}\:{maximum}\:{ab}\:+{bc}\:+{ca}\: \\ $$$${a}\:,\:{b}\:,\:{c}\:{are}\:{non}\:{negative}\:{integers} \\ $$$$ \\ $$

Answered by Frix last updated on 16/Jun/23

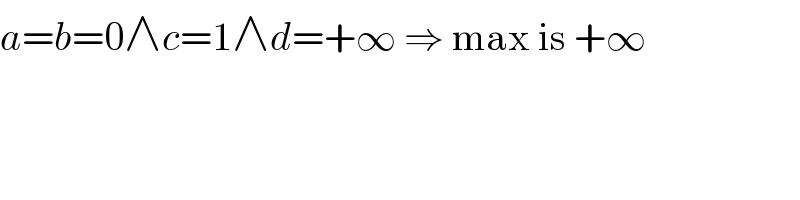
a=b=0∧c=1∧d=+∞ ⇒ max is +∞

$${a}={b}=\mathrm{0}\wedge{c}=\mathrm{1}\wedge{d}=+\infty\:\Rightarrow\:\mathrm{max}\:\mathrm{is}\:+\infty \\ $$

Commented by York12 last updated on 16/Jun/23

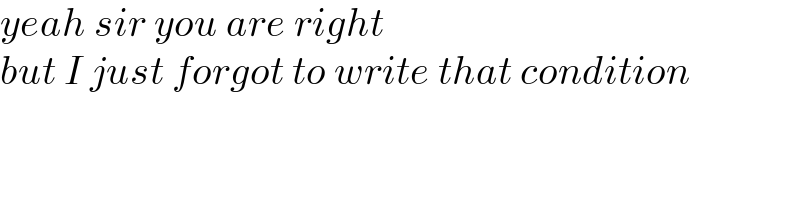
yeah sir you are right but I just forgot to write that condition

$${yeah}\:{sir}\:{you}\:{are}\:{right} \\ $$$${but}\:{I}\:{just}\:{forgot}\:{to}\:{write}\:{that}\:{condition} \\ $$$$ \\ $$

Answered by Subhi last updated on 16/Jun/23

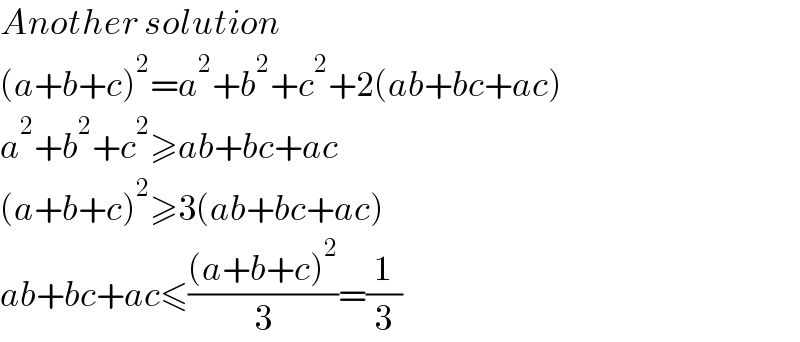
Another solution (a+b+c)^2 =a^2 +b^2 +c^2 +2(ab+bc+ac) a^2 +b^2 +c^2 ≥ab+bc+ac (a+b+c)^2 ≥3(ab+bc+ac) ab+bc+ac≤(((a+b+c)^2 )/3)=(1/3)

$${Another}\:{solution} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ac}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \geqslant{ab}+{bc}+{ac} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} \geqslant\mathrm{3}\left({ab}+{bc}+{ac}\right) \\ $$$${ab}+{bc}+{ac}\leqslant\frac{\left({a}+{b}+{c}\right)^{\mathrm{2}} }{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Commented by York12 last updated on 16/Jun/23

thnx

$${thnx} \\ $$

Commented by York12 last updated on 17/Jun/23

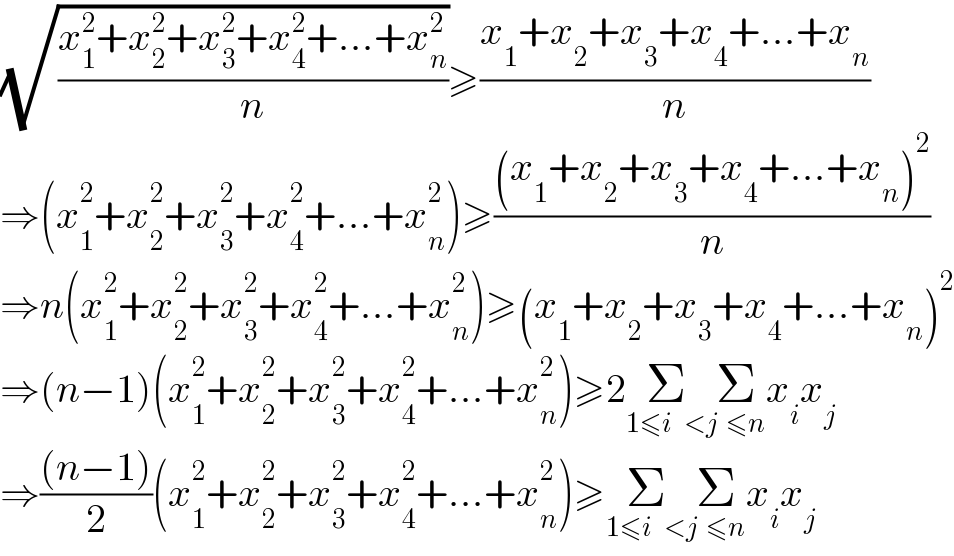
(√((x_1 ^2 +x_2 ^2 +x_3 ^2 +x_4 ^2 +...+x_n ^2 )/n))≥((x_1 +x_2 +x_3 +x_4 +...+x_n )/n) ⇒(x_1 ^2 +x_2 ^2 +x_3 ^2 +x_4 ^2 +...+x_n ^2 )≥(((x_1 +x_2 +x_3 +x_4 +...+x_n )^2 )/n) ⇒n(x_1 ^2 +x_2 ^2 +x_3 ^2 +x_4 ^2 +...+x_n ^2 )≥(x_1 +x_2 +x_3 +x_4 +...+x_n )^2 ⇒(n−1)(x_1 ^2 +x_2 ^2 +x_3 ^2 +x_4 ^2 +...+x_n ^2 )≥2Σ_(1≤i <) Σ_(j ≤n) x_i x_j ⇒(((n−1))/2)(x_1 ^2 +x_2 ^2 +x_3 ^2 +x_4 ^2 +...+x_n ^2 )≥Σ_(1≤i <) Σ_(j ≤n) x_i x_j

$$\sqrt{\frac{{x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} +{x}_{\mathrm{4}} ^{\mathrm{2}} +...+{x}_{{n}} ^{\mathrm{2}} }{{n}}}\geqslant\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} +...+{x}_{{n}} }{{n}} \\ $$$$\Rightarrow\left({x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} +{x}_{\mathrm{4}} ^{\mathrm{2}} +...+{x}_{{n}} ^{\mathrm{2}} \right)\geqslant\frac{\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} +...+{x}_{{n}} \right)^{\mathrm{2}} }{{n}} \\ $$$$\Rightarrow{n}\left({x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} +{x}_{\mathrm{4}} ^{\mathrm{2}} +...+{x}_{{n}} ^{\mathrm{2}} \right)\geqslant\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} +...+{x}_{{n}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\left({n}−\mathrm{1}\right)\left({x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} +{x}_{\mathrm{4}} ^{\mathrm{2}} +...+{x}_{{n}} ^{\mathrm{2}} \right)\geqslant\mathrm{2}\underset{\mathrm{1}\leqslant{i}\:\:\:<} {\sum}\underset{{j}\:\:\leqslant{n}} {\sum}{x}_{{i}} {x}_{{j}} \\ $$$$\Rightarrow\frac{\left({n}−\mathrm{1}\right)}{\mathrm{2}}\left({x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} +{x}_{\mathrm{4}} ^{\mathrm{2}} +...+{x}_{{n}} ^{\mathrm{2}} \right)\geqslant\underset{\mathrm{1}\leqslant{i}\:\:\:<} {\sum}\underset{{j}\:\:\leqslant{n}} {\sum}{x}_{{i}} {x}_{{j}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com