Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 159394 by azadsir last updated on 16/Nov/21

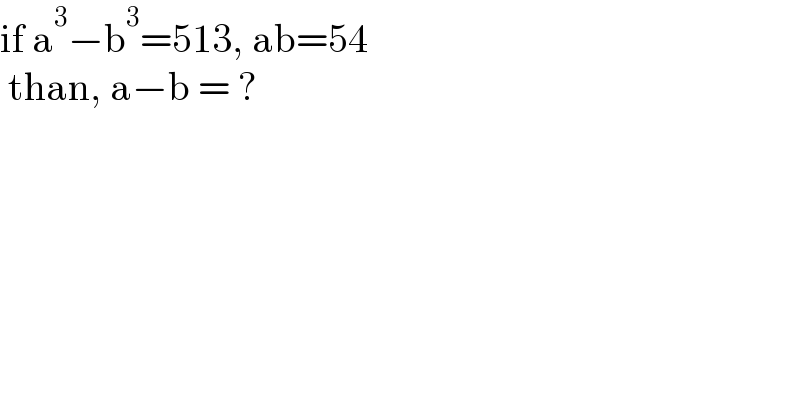
if a^3 −b^3 =513, ab=54 than, a−b = ?

$$\mathrm{if}\:\mathrm{a}^{\mathrm{3}} −\mathrm{b}^{\mathrm{3}} =\mathrm{513},\:\mathrm{ab}=\mathrm{54} \\ $$$$\:\mathrm{than},\:\mathrm{a}−\mathrm{b}\:=\:? \\ $$

Commented by cortano last updated on 16/Nov/21

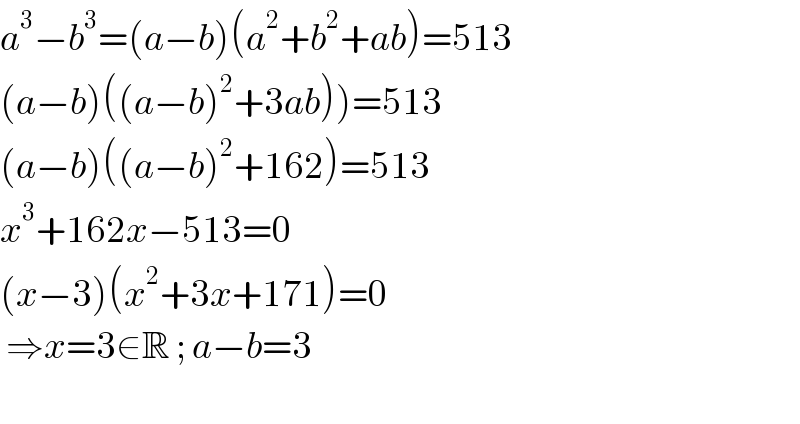
a^3 −b^3 =(a−b)(a^2 +b^2 +ab)=513 (a−b)((a−b)^2 +3ab))=513 (a−b)((a−b)^2 +162)=513 x^3 +162x−513=0 (x−3)(x^2 +3x+171)=0 ⇒x=3∈R ; a−b=3

$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\right)=\mathrm{513} \\ $$$$\left.\left({a}−{b}\right)\left(\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{3}{ab}\right)\right)=\mathrm{513} \\ $$$$\left({a}−{b}\right)\left(\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{162}\right)=\mathrm{513} \\ $$$${x}^{\mathrm{3}} +\mathrm{162}{x}−\mathrm{513}=\mathrm{0} \\ $$$$\left({x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{171}\right)=\mathrm{0} \\ $$$$\:\Rightarrow{x}=\mathrm{3}\in\mathbb{R}\:;\:{a}−{b}=\mathrm{3} \\ $$$$ \\ $$

Commented by azadsir last updated on 16/Nov/21

Thank you

$$\mathrm{Thank}\:\mathrm{you} \\ $$

Answered by Rasheed.Sindhi last updated on 16/Nov/21

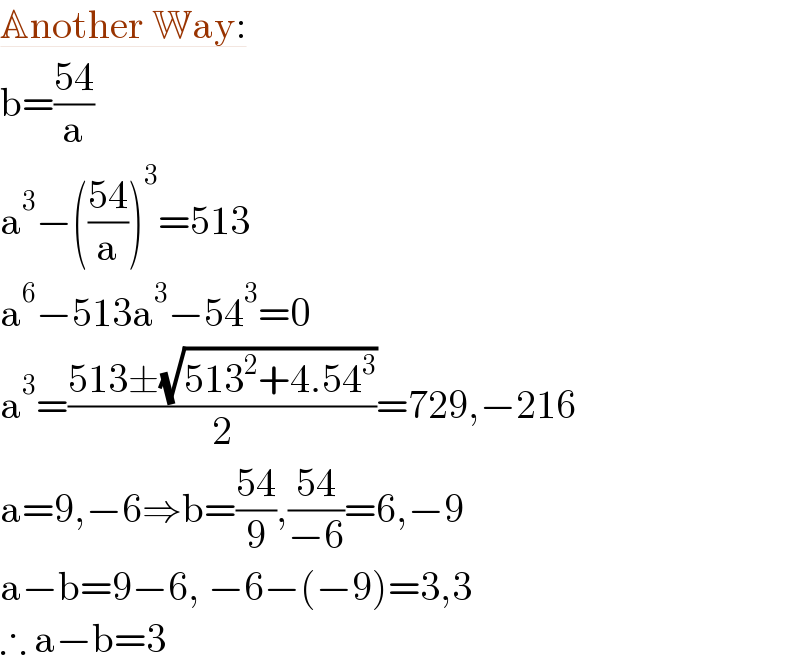
Another Way: b=((54)/a) a^3 −(((54)/a))^3 =513 a^6 −513a^3 −54^3 =0 a^3 =((513±(√(513^2 +4.54^3 )))/2)=729,−216 a=9,−6⇒b=((54)/9),((54)/(−6))=6,−9 a−b=9−6, −6−(−9)=3,3 ∴ a−b=3

$$\underline{\mathbb{A}\mathrm{nother}\:\mathbb{W}\mathrm{ay}:} \\ $$$$\mathrm{b}=\frac{\mathrm{54}}{\mathrm{a}} \\ $$$$\mathrm{a}^{\mathrm{3}} −\left(\frac{\mathrm{54}}{\mathrm{a}}\right)^{\mathrm{3}} =\mathrm{513} \\ $$$$\mathrm{a}^{\mathrm{6}} −\mathrm{513a}^{\mathrm{3}} −\mathrm{54}^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{a}^{\mathrm{3}} =\frac{\mathrm{513}\pm\sqrt{\mathrm{513}^{\mathrm{2}} +\mathrm{4}.\mathrm{54}^{\mathrm{3}} }}{\mathrm{2}}=\mathrm{729},−\mathrm{216} \\ $$$$\mathrm{a}=\mathrm{9},−\mathrm{6}\Rightarrow\mathrm{b}=\frac{\mathrm{54}}{\mathrm{9}},\frac{\mathrm{54}}{−\mathrm{6}}=\mathrm{6},−\mathrm{9} \\ $$$$\mathrm{a}−\mathrm{b}=\mathrm{9}−\mathrm{6},\:−\mathrm{6}−\left(−\mathrm{9}\right)=\mathrm{3},\mathrm{3} \\ $$$$\therefore\:\mathrm{a}−\mathrm{b}=\mathrm{3} \\ $$

Answered by Rasheed.Sindhi last updated on 16/Nov/21

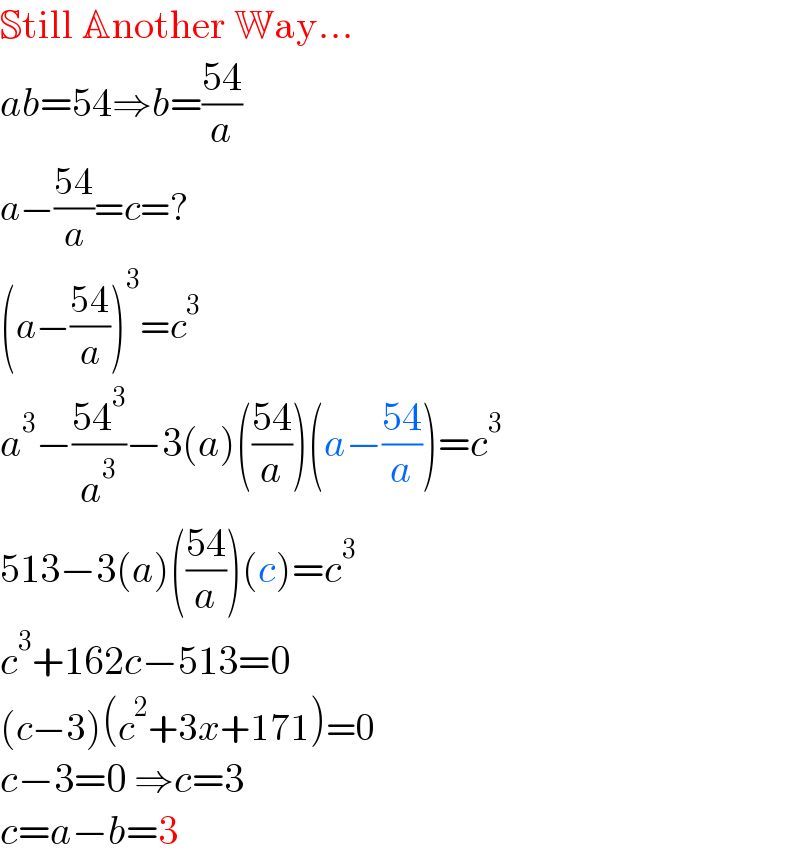
Still Another Way... ab=54⇒b=((54)/a) a−((54)/a)=c=? (a−((54)/a))^3 =c^3 a^3 −((54^3 )/a^3 )−3(a)(((54)/a))(a−((54)/a))=c^3 513−3(a)(((54)/a))(c)=c^3 c^3 +162c−513=0 (c−3)(c^2 +3x+171)=0 c−3=0 ⇒c=3 c=a−b=3

$$\mathbb{S}\mathrm{till}\:\mathbb{A}\mathrm{nother}\:\mathbb{W}\mathrm{ay}... \\ $$$${ab}=\mathrm{54}\Rightarrow{b}=\frac{\mathrm{54}}{{a}} \\ $$$${a}−\frac{\mathrm{54}}{{a}}={c}=? \\ $$$$\left({a}−\frac{\mathrm{54}}{{a}}\right)^{\mathrm{3}} ={c}^{\mathrm{3}} \\ $$$${a}^{\mathrm{3}} −\frac{\mathrm{54}^{\mathrm{3}} }{{a}^{\mathrm{3}} }−\mathrm{3}\left({a}\right)\left(\frac{\mathrm{54}}{{a}}\right)\left({a}−\frac{\mathrm{54}}{{a}}\right)={c}^{\mathrm{3}} \\ $$$$\mathrm{513}−\mathrm{3}\left({a}\right)\left(\frac{\mathrm{54}}{{a}}\right)\left({c}\right)={c}^{\mathrm{3}} \\ $$$${c}^{\mathrm{3}} +\mathrm{162}{c}−\mathrm{513}=\mathrm{0} \\ $$$$\left({c}−\mathrm{3}\right)\left({c}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{171}\right)=\mathrm{0} \\ $$$${c}−\mathrm{3}=\mathrm{0}\:\Rightarrow{c}=\mathrm{3} \\ $$$${c}={a}−{b}=\mathrm{3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com