
Question Number 63858 by gunawan last updated on 10/Jul/19
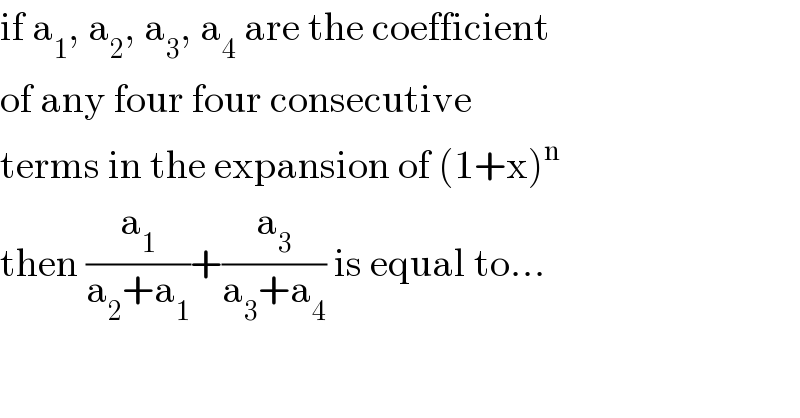
$$\mathrm{if}\:\mathrm{a}_{\mathrm{1}} ,\:\mathrm{a}_{\mathrm{2}} ,\:\mathrm{a}_{\mathrm{3}} ,\:\mathrm{a}_{\mathrm{4}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{coefficient} \\ $$$$\mathrm{of}\:\mathrm{any}\:\mathrm{four}\:\mathrm{four}\:\mathrm{consecutive} \\ $$$$\mathrm{terms}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} \\ $$$$\mathrm{then}\:\frac{\mathrm{a}_{\mathrm{1}} }{\mathrm{a}_{\mathrm{2}} +\mathrm{a}_{\mathrm{1}} }+\frac{\mathrm{a}_{\mathrm{3}} }{\mathrm{a}_{\mathrm{3}} +\mathrm{a}_{\mathrm{4}} }\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}... \\ $$
Answered by ajfour last updated on 10/Jul/19
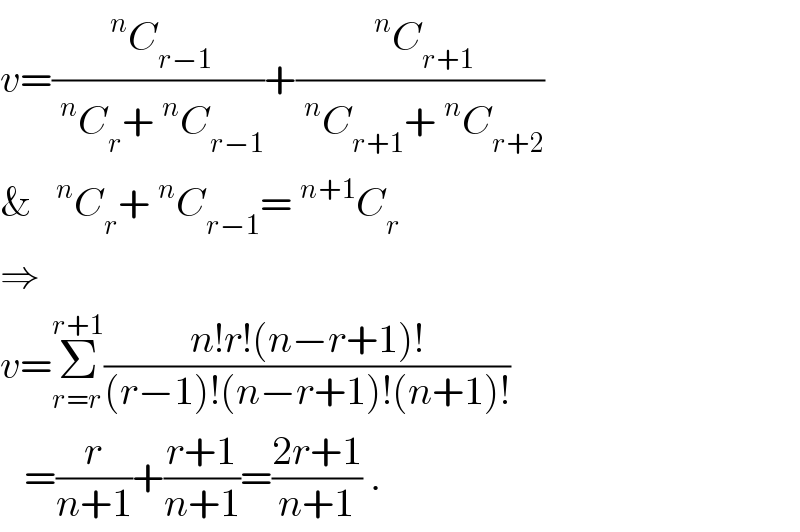
$${v}=\frac{\:^{{n}} {C}_{{r}−\mathrm{1}} }{\:^{{n}} {C}_{{r}} +\:^{{n}} {C}_{{r}−\mathrm{1}} }+\frac{\:^{{n}} {C}_{{r}+\mathrm{1}} }{\:^{{n}} {C}_{{r}+\mathrm{1}} +\:^{{n}} {C}_{{r}+\mathrm{2}} } \\ $$$$\&\:\:\:^{{n}} {C}_{{r}} +\:^{{n}} {C}_{{r}−\mathrm{1}} =\:^{{n}+\mathrm{1}} {C}_{{r}} \\ $$$$\Rightarrow \\ $$$${v}=\underset{{r}={r}} {\overset{{r}+\mathrm{1}} {\sum}}\frac{{n}!{r}!\left({n}−{r}+\mathrm{1}\right)!}{\left({r}−\mathrm{1}\right)!\left({n}−{r}+\mathrm{1}\right)!\left({n}+\mathrm{1}\right)!} \\ $$$$\:\:\:=\frac{{r}}{{n}+\mathrm{1}}+\frac{{r}+\mathrm{1}}{{n}+\mathrm{1}}=\frac{\mathrm{2}{r}+\mathrm{1}}{{n}+\mathrm{1}}\:. \\ $$
