
Question Number 113983 by mohammad17 last updated on 16/Sep/20

$${if}\:{Z}_{\mathrm{1}} =\mathrm{1}−{i}\:{and}\:{Z}_{\mathrm{2}} ={i}^{\mathrm{4}} \:{by}\:{using}\:{demover}\:{find}\:\frac{{Z}_{\mathrm{1}} }{{Z}_{\mathrm{2}} }\:? \\ $$
Answered by Dwaipayan Shikari last updated on 16/Sep/20

$$\frac{{Z}_{\mathrm{1}} }{{Z}_{\mathrm{2}} }=\frac{\mathrm{1}−{i}}{{i}^{\mathrm{4}} }=\mathrm{1}−{i} \\ $$
Commented by mohammad17 last updated on 16/Sep/20
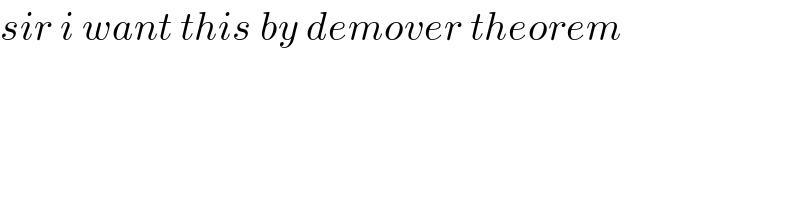
$${sir}\:{i}\:{want}\:{this}\:{by}\:{demover}\:{theorem}\: \\ $$
Answered by Dwaipayan Shikari last updated on 16/Sep/20
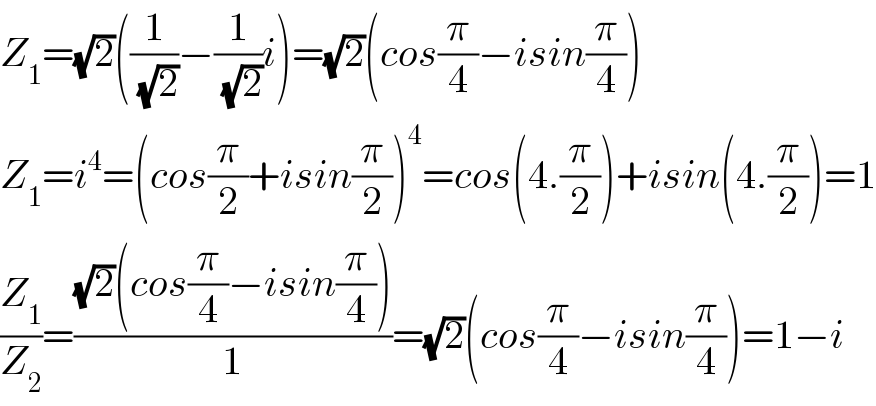
$${Z}_{\mathrm{1}} =\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{i}\right)=\sqrt{\mathrm{2}}\left({cos}\frac{\pi}{\mathrm{4}}−{isin}\frac{\pi}{\mathrm{4}}\right) \\ $$$${Z}_{\mathrm{1}} ={i}^{\mathrm{4}} =\left({cos}\frac{\pi}{\mathrm{2}}+{isin}\frac{\pi}{\mathrm{2}}\right)^{\mathrm{4}} ={cos}\left(\mathrm{4}.\frac{\pi}{\mathrm{2}}\right)+{isin}\left(\mathrm{4}.\frac{\pi}{\mathrm{2}}\right)=\mathrm{1} \\ $$$$\frac{{Z}_{\mathrm{1}} }{{Z}_{\mathrm{2}} }=\frac{\sqrt{\mathrm{2}}\left({cos}\frac{\pi}{\mathrm{4}}−{isin}\frac{\pi}{\mathrm{4}}\right)}{\mathrm{1}}=\sqrt{\mathrm{2}}\left({cos}\frac{\pi}{\mathrm{4}}−{isin}\frac{\pi}{\mathrm{4}}\right)=\mathrm{1}−{i} \\ $$
Commented by mohammad17 last updated on 16/Sep/20

$${thank}\:{you}\:{sir} \\ $$
