
Question Number 147882 by mathdanisur last updated on 24/Jul/21
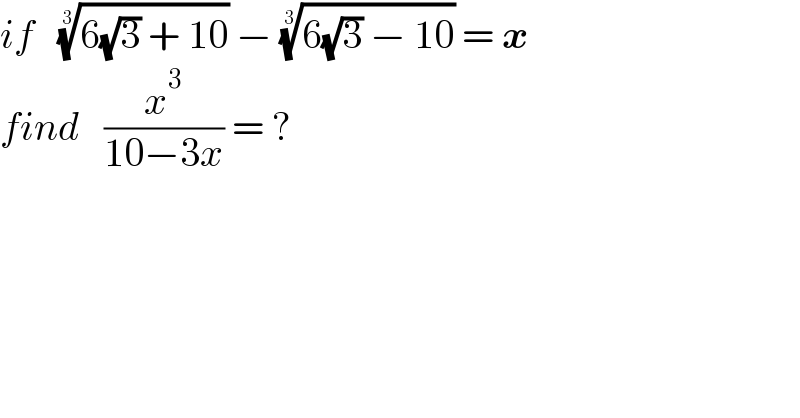
$${if}\:\:\:\sqrt[{\mathrm{3}}]{\mathrm{6}\sqrt{\mathrm{3}}\:+\:\mathrm{10}}\:−\:\sqrt[{\mathrm{3}}]{\mathrm{6}\sqrt{\mathrm{3}}\:−\:\mathrm{10}}\:=\:\boldsymbol{{x}} \\ $$$${find}\:\:\:\frac{{x}^{\mathrm{3}} }{\mathrm{10}−\mathrm{3}{x}}\:=\:? \\ $$
Answered by mr W last updated on 24/Jul/21
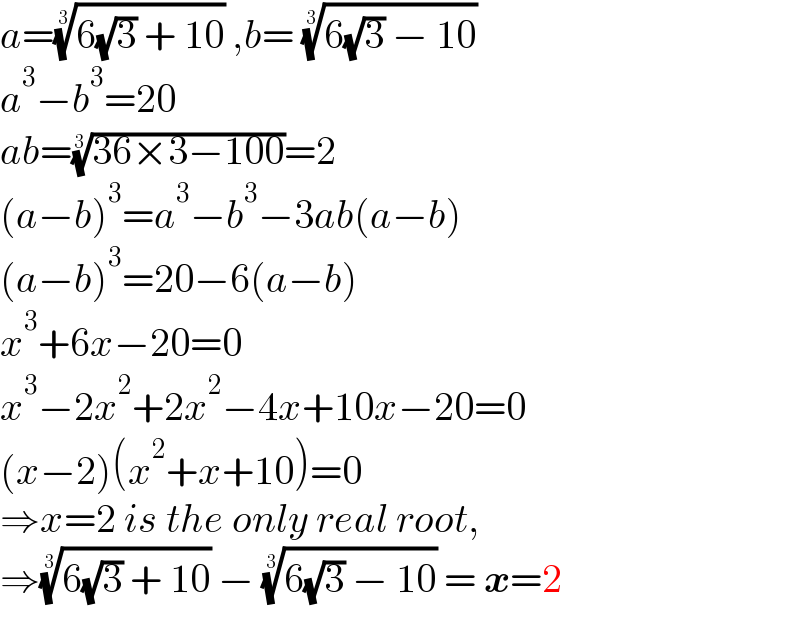
$${a}=\sqrt[{\mathrm{3}}]{\mathrm{6}\sqrt{\mathrm{3}}\:+\:\mathrm{10}}\:,{b}=\:\sqrt[{\mathrm{3}}]{\mathrm{6}\sqrt{\mathrm{3}}\:−\:\mathrm{10}} \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\mathrm{20} \\ $$$${ab}=\sqrt[{\mathrm{3}}]{\mathrm{36}×\mathrm{3}−\mathrm{100}}=\mathrm{2} \\ $$$$\left({a}−{b}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} −{b}^{\mathrm{3}} −\mathrm{3}{ab}\left({a}−{b}\right) \\ $$$$\left({a}−{b}\right)^{\mathrm{3}} =\mathrm{20}−\mathrm{6}\left({a}−{b}\right) \\ $$$${x}^{\mathrm{3}} +\mathrm{6}{x}−\mathrm{20}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{10}{x}−\mathrm{20}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{10}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{2}\:{is}\:{the}\:{only}\:{real}\:{root}, \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{\mathrm{6}\sqrt{\mathrm{3}}\:+\:\mathrm{10}}\:−\:\sqrt[{\mathrm{3}}]{\mathrm{6}\sqrt{\mathrm{3}}\:−\:\mathrm{10}}\:=\:\boldsymbol{{x}}=\mathrm{2} \\ $$
Commented by mathdanisur last updated on 24/Jul/21

$${Thankyou}\:{Sir} \\ $$
Answered by behi834171 last updated on 24/Jul/21
![{ ((ab=2)),((a−b=x [a=(6(√3)+10)^(1/3) ,b=(6(√3)−10)^(1/3) ])),((a^3 −b^3 =20)) :} ⇒(a−b)[(a−b)^2 +3ab]=20 ⇒x(x^2 +6)=20⇒x^3 +6x−20=0 ⇒(x−2)(x^2 +2x+10)=0⇒x=2 ⇒(x^3 /(10−3x))=(8/(10−6))=2 .■](Q147916.png)
$$\begin{cases}{{ab}=\mathrm{2}}\\{{a}−{b}={x}\:\:\:\:\:\:\:\:\left[{a}=\left(\mathrm{6}\sqrt{\mathrm{3}}+\mathrm{10}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ,{b}=\left(\mathrm{6}\sqrt{\mathrm{3}}−\mathrm{10}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right]}\\{{a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\mathrm{20}}\end{cases} \\ $$$$\Rightarrow\left({a}−{b}\right)\left[\left({a}−{b}\right)^{\mathrm{2}} +\mathrm{3}{ab}\right]=\mathrm{20} \\ $$$$\Rightarrow{x}\left({x}^{\mathrm{2}} +\mathrm{6}\right)=\mathrm{20}\Rightarrow{x}^{\mathrm{3}} +\mathrm{6}{x}−\mathrm{20}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}\right)=\mathrm{0}\Rightarrow{x}=\mathrm{2} \\ $$$$\Rightarrow\frac{{x}^{\mathrm{3}} }{\mathrm{10}−\mathrm{3}{x}}=\frac{\mathrm{8}}{\mathrm{10}−\mathrm{6}}=\mathrm{2}\:\:\:\:\:\:\:\:.\blacksquare \\ $$
Commented by mathdanisur last updated on 24/Jul/21

$${Thankyou}\:{Sir} \\ $$
