
Question Number 188384 by universe last updated on 28/Feb/23
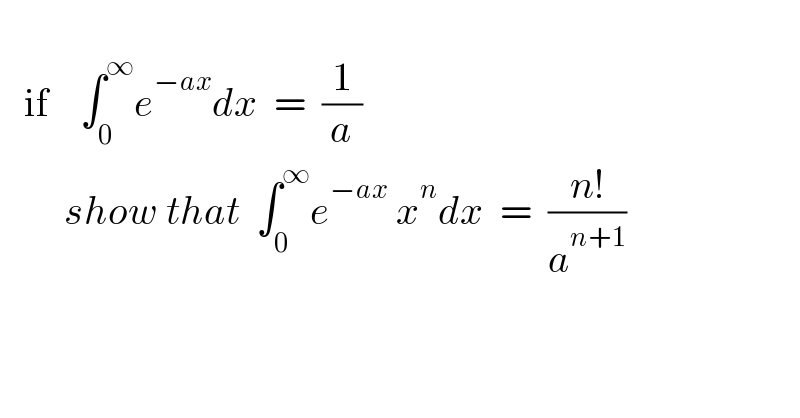
$$\:\:\: \\ $$$$\:\:\:\mathrm{if}\:\:\:\:\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} {dx}\:\:=\:\:\frac{\mathrm{1}}{{a}} \\ $$$$\:\:\:\:\:\:\:\:{show}\:{that}\:\:\int_{\mathrm{0}} ^{\infty} {e}^{−{ax}} \:{x}^{{n}} {dx}\:\:=\:\:\frac{{n}!}{{a}^{{n}+\mathrm{1}} } \\ $$
Answered by qaz last updated on 28/Feb/23
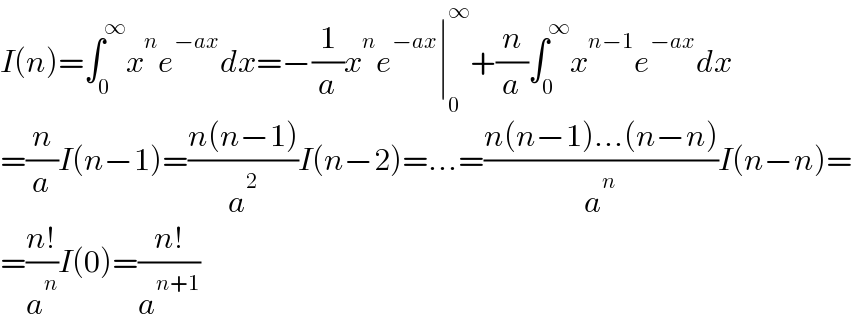
$${I}\left({n}\right)=\int_{\mathrm{0}} ^{\infty} {x}^{{n}} {e}^{−{ax}} {dx}=−\frac{\mathrm{1}}{{a}}{x}^{{n}} {e}^{−{ax}} \mid_{\mathrm{0}} ^{\infty} +\frac{{n}}{{a}}\int_{\mathrm{0}} ^{\infty} {x}^{{n}−\mathrm{1}} {e}^{−{ax}} {dx} \\ $$$$=\frac{{n}}{{a}}{I}\left({n}−\mathrm{1}\right)=\frac{{n}\left({n}−\mathrm{1}\right)}{{a}^{\mathrm{2}} }{I}\left({n}−\mathrm{2}\right)=...=\frac{{n}\left({n}−\mathrm{1}\right)...\left({n}−{n}\right)}{{a}^{{n}} }{I}\left({n}−{n}\right)= \\ $$$$=\frac{{n}!}{{a}^{{n}} }{I}\left(\mathrm{0}\right)=\frac{{n}!}{{a}^{{n}+\mathrm{1}} } \\ $$
