
Question Number 53688 by kwonjun1202 last updated on 25/Jan/19
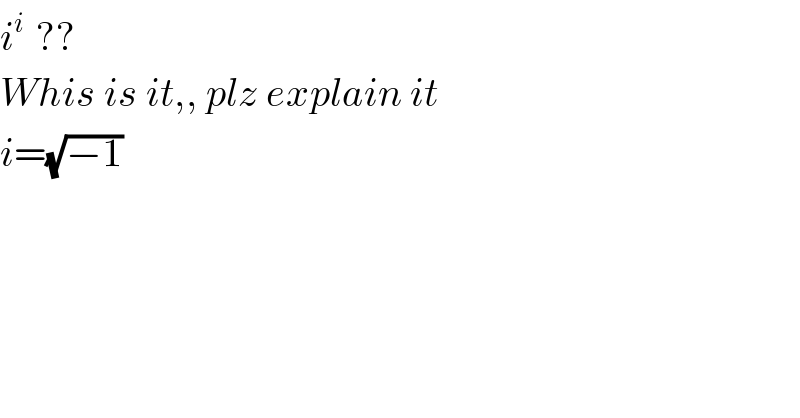
$${i}^{{i}\:} \:?? \\ $$$${Whis}\:{is}\:{it},,\:{plz}\:{explain}\:{it} \\ $$$${i}=\sqrt{−\mathrm{1}} \\ $$
Commented by Abdo msup. last updated on 25/Jan/19
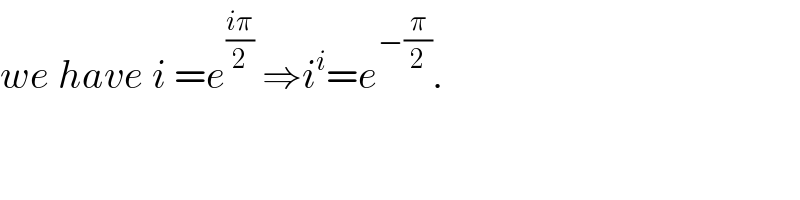
$${we}\:{have}\:{i}\:={e}^{\frac{{i}\pi}{\mathrm{2}}} \:\Rightarrow{i}^{{i}} ={e}^{−\frac{\pi}{\mathrm{2}}} . \\ $$
Answered by MJS last updated on 25/Jan/19
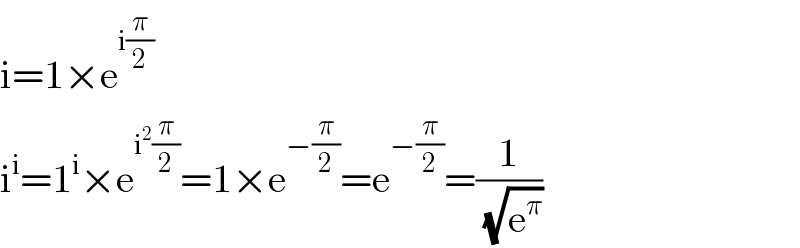
$$\mathrm{i}=\mathrm{1}×\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{i}^{\mathrm{i}} =\mathrm{1}^{\mathrm{i}} ×\mathrm{e}^{\mathrm{i}^{\mathrm{2}} \frac{\pi}{\mathrm{2}}} =\mathrm{1}×\mathrm{e}^{−\frac{\pi}{\mathrm{2}}} =\mathrm{e}^{−\frac{\pi}{\mathrm{2}}} =\frac{\mathrm{1}}{\sqrt{\mathrm{e}^{\pi} }} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jan/19
![we know a^x =e^(xlog_e a) now i^i =e^(iLog_e i) =e^(iLog(0+1×i)) now formula Log_e (α+iβ)=log_e (α+iβ)+i2πn =[log_e (√(α^2 +β^2 )) +itan^(−1) ((β/α))]+i2πn Log_e (α+iβ) =(1/2)log_e (α^2 +β^2 )+i{2πn+tan^(−1) ((β/α))} so as per problem α=0 β=1 so value of Log_e (0+i) =(1/2)log_e (0^2 +1^2 )+i{2πn+tan^(−1) ((1/0))} =(1/2)×0+i{2πn+(π/2)} now i^i =e^(iLog_e i) =e^(i{(2πn+(π/2))i}) =e^((2πn+(π/2))×−1) =e^(−(2πn+(π/2))) =e^(−(π/2)) principle value](Q53703.png)
$${we}\:{know}\:{a}^{{x}} ={e}^{{xlog}_{{e}} {a}} \\ $$$${now}\:\:{i}^{{i}} ={e}^{{iLog}_{{e}} {i}} ={e}^{{iLog}\left(\mathrm{0}+\mathrm{1}×{i}\right)} \\ $$$${now}\:{formula} \\ $$$${Log}_{{e}} \left(\alpha+{i}\beta\right)={log}_{{e}} \left(\alpha+{i}\beta\right)+{i}\mathrm{2}\pi{n} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[{log}_{{e}} \sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }\:+{itan}^{−\mathrm{1}} \left(\frac{\beta}{\alpha}\right)\right]+{i}\mathrm{2}\pi{n} \\ $$$${Log}_{{e}} \left(\alpha+{i}\beta\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}_{{e}} \left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)+{i}\left\{\mathrm{2}\pi{n}+{tan}^{−\mathrm{1}} \left(\frac{\beta}{\alpha}\right)\right\} \\ $$$${so}\:{as}\:{per}\:{problem}\:\alpha=\mathrm{0}\:\:\:\:\beta=\mathrm{1} \\ $$$${so}\:{value}\:{of}\:{Log}_{{e}} \left(\mathrm{0}+{i}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}_{{e}} \left(\mathrm{0}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} \right)+{i}\left\{\mathrm{2}\pi{n}+{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{0}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{0}+{i}\left\{\mathrm{2}\pi{n}+\frac{\pi}{\mathrm{2}}\right\} \\ $$$${now}\: \\ $$$${i}^{{i}} ={e}^{{iLog}_{{e}} {i}} \\ $$$$\:={e}^{{i}\left\{\left(\mathrm{2}\pi{n}+\frac{\pi}{\mathrm{2}}\right){i}\right\}} \\ $$$$={e}^{\left(\mathrm{2}\pi{n}+\frac{\pi}{\mathrm{2}}\right)×−\mathrm{1}} \\ $$$$={e}^{−\left(\mathrm{2}\pi{n}+\frac{\pi}{\mathrm{2}}\right)} \\ $$$$={e}^{−\frac{\pi}{\mathrm{2}}} \:\:{principle}\:{value} \\ $$$$ \\ $$
