
Question Number 109005 by Study last updated on 20/Aug/20

$${i}^{{i}} =? \\ $$
Answered by floor(10²Eta[1]) last updated on 20/Aug/20
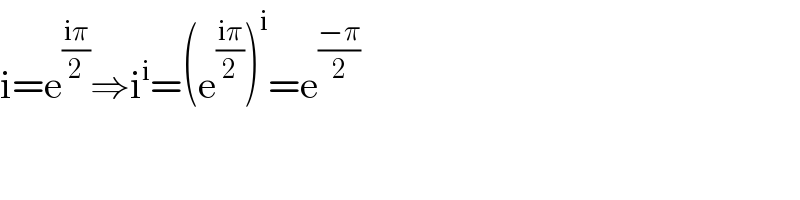
$$\mathrm{i}=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \Rightarrow\mathrm{i}^{\mathrm{i}} =\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)^{\mathrm{i}} =\mathrm{e}^{\frac{−\pi}{\mathrm{2}}} \\ $$
Answered by Dwaipayan Shikari last updated on 20/Aug/20
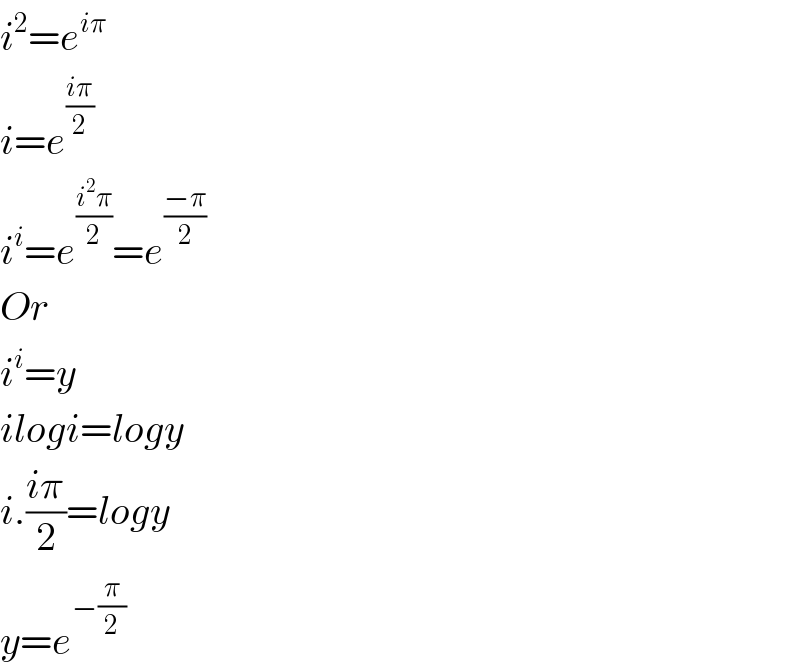
$${i}^{\mathrm{2}} ={e}^{{i}\pi} \\ $$$${i}={e}^{\frac{{i}\pi}{\mathrm{2}}} \\ $$$${i}^{{i}} ={e}^{\frac{{i}^{\mathrm{2}} \pi}{\mathrm{2}}} ={e}^{\frac{−\pi}{\mathrm{2}}} \\ $$$${Or} \\ $$$${i}^{{i}} ={y} \\ $$$${ilogi}={logy} \\ $$$${i}.\frac{{i}\pi}{\mathrm{2}}={logy} \\ $$$${y}={e}^{−\frac{\pi}{\mathrm{2}}} \\ $$
