
Question Number 212765 by issac last updated on 23/Oct/24

$$\mathrm{i}\:\:\mathrm{generalized}\:\boldsymbol{\mathrm{Bessel}}\:\boldsymbol{\mathrm{function}}'\mathrm{s} \\ $$$$\mathrm{Laplace}\:\mathrm{Transform} \\ $$$$\mathrm{L}.\mathrm{T}{J}_{\nu} \left({z}\right)=\frac{\left({s}+\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}\right)^{−\nu} }{\:\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}}\:,\:{s}\in\left[\mathrm{0},\infty\right)\:,\:\nu\in\mathbb{R} \\ $$$$\mathrm{L}.\mathrm{T}\:{Y}_{\nu} \left({z}\right)=\frac{\mathrm{cot}\left(\pi\nu\right)\left({s}+\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}\right)^{−\nu} }{\:\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}}−\frac{\mathrm{csc}\left(\pi\nu\right)\left({s}+\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}\right)^{\nu} }{\:\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${s}\in\left[\mathrm{0},\infty\right)\:,\:\nu\in\mathbb{R}^{+} \backslash\left\{\mathrm{0},\mathbb{Z}^{+} \right\} \\ $$$$\mathrm{but}....\:\mathrm{i}\:\mathrm{can}'\mathrm{t}\:\mathrm{explain}\:\mathrm{why}\:\mathrm{L}.\mathrm{T}\:{Y}_{\nu} \left({z}\right) \\ $$$$\mathrm{is}\:\mathrm{undefined}\:\mathrm{when}\:\nu\in\mathbb{Z}^{+} \backslash\left\{\mathrm{0}\right\}..... \\ $$$$\mathrm{Help}\:\mathrm{me}.....!!! \\ $$
Answered by Frix last updated on 23/Oct/24
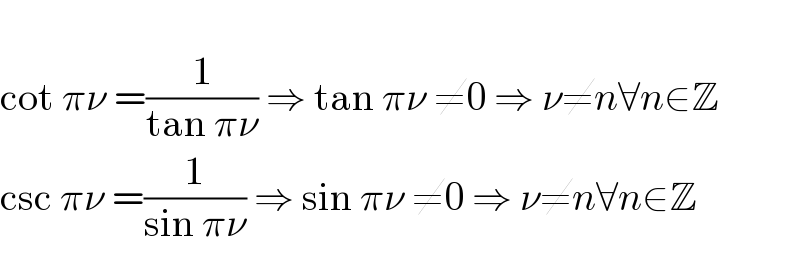
$$ \\ $$$$\mathrm{cot}\:\pi\nu\:=\frac{\mathrm{1}}{\mathrm{tan}\:\pi\nu}\:\Rightarrow\:\mathrm{tan}\:\pi\nu\:\neq\mathrm{0}\:\Rightarrow\:\nu\neq{n}\forall{n}\in\mathbb{Z} \\ $$$$\mathrm{csc}\:\pi\nu\:=\frac{\mathrm{1}}{\mathrm{sin}\:\pi\nu}\:\Rightarrow\:\mathrm{sin}\:\pi\nu\:\neq\mathrm{0}\:\Rightarrow\:\nu\neq{n}\forall{n}\in\mathbb{Z} \\ $$
