Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 116770 by bounhome last updated on 06/Oct/20

how to prove the Pythagorean theorem(c^2 =a^2 +b^2 )

$${how}\:{to}\:{prove}\:{the}\:{Pythagorean}\:{theorem}\left({c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$

Commented by $@y@m last updated on 06/Oct/20

https://www.math-only-math.com/proof-of-pythagorean-theorem.html#:~:text=The%20proof%20of%20Pythagorean%20Theorem,of%20c%20(c2).

Answered by MJS_new last updated on 06/Oct/20

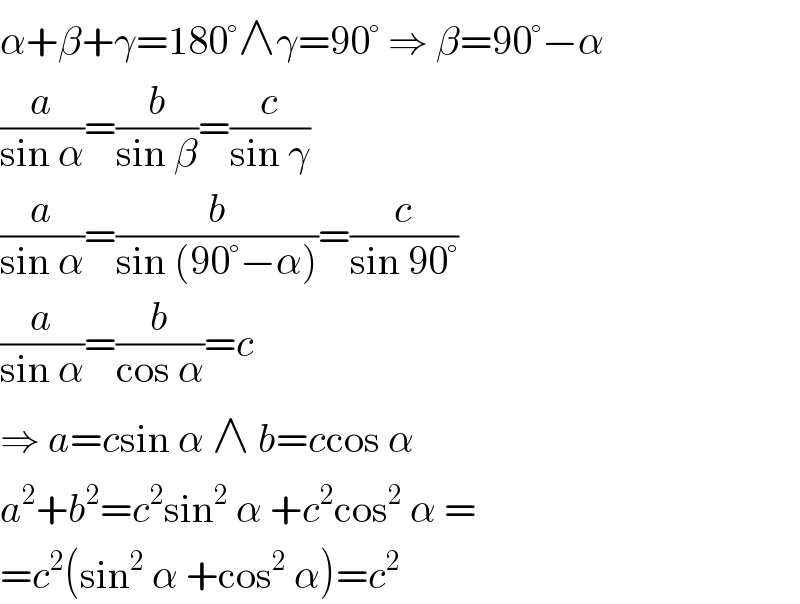
α+β+γ=180°∧γ=90° ⇒ β=90°−α (a/(sin α))=(b/(sin β))=(c/(sin γ)) (a/(sin α))=(b/(sin (90°−α)))=(c/(sin 90°)) (a/(sin α))=(b/(cos α))=c ⇒ a=csin α ∧ b=ccos α a^2 +b^2 =c^2 sin^2 α +c^2 cos^2 α = =c^2 (sin^2 α +cos^2 α)=c^2

$$\alpha+\beta+\gamma=\mathrm{180}°\wedge\gamma=\mathrm{90}°\:\Rightarrow\:\beta=\mathrm{90}°−\alpha \\ $$$$\frac{{a}}{\mathrm{sin}\:\alpha}=\frac{{b}}{\mathrm{sin}\:\beta}=\frac{{c}}{\mathrm{sin}\:\gamma} \\ $$$$\frac{{a}}{\mathrm{sin}\:\alpha}=\frac{{b}}{\mathrm{sin}\:\left(\mathrm{90}°−\alpha\right)}=\frac{{c}}{\mathrm{sin}\:\mathrm{90}°} \\ $$$$\frac{{a}}{\mathrm{sin}\:\alpha}=\frac{{b}}{\mathrm{cos}\:\alpha}={c} \\ $$$$\Rightarrow\:{a}={c}\mathrm{sin}\:\alpha\:\wedge\:{b}={c}\mathrm{cos}\:\alpha \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha\:+{c}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha\:= \\ $$$$={c}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \:\alpha\:+\mathrm{cos}^{\mathrm{2}} \:\alpha\right)={c}^{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com