Question Number 153420 by alcohol last updated on 07/Sep/21
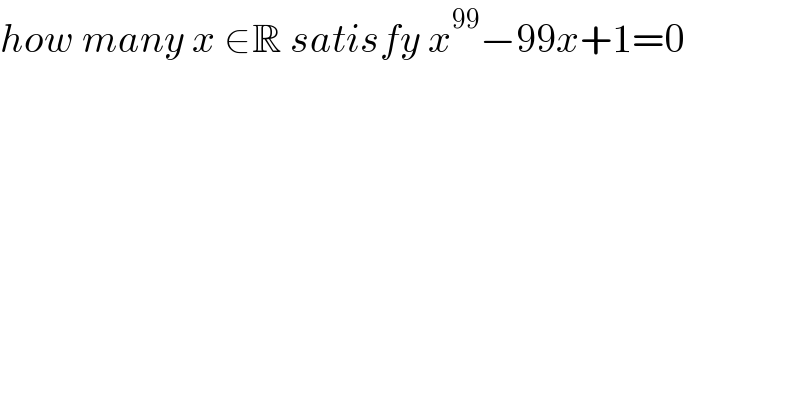
$${how}\:{many}\:{x}\:\in\mathbb{R}\:{satisfy}\:{x}^{\mathrm{99}} −\mathrm{99}{x}+\mathrm{1}=\mathrm{0} \\ $$
Answered by mr W last updated on 07/Sep/21
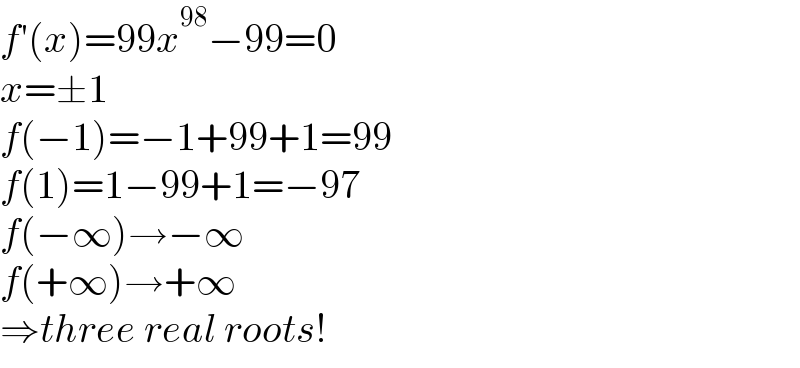
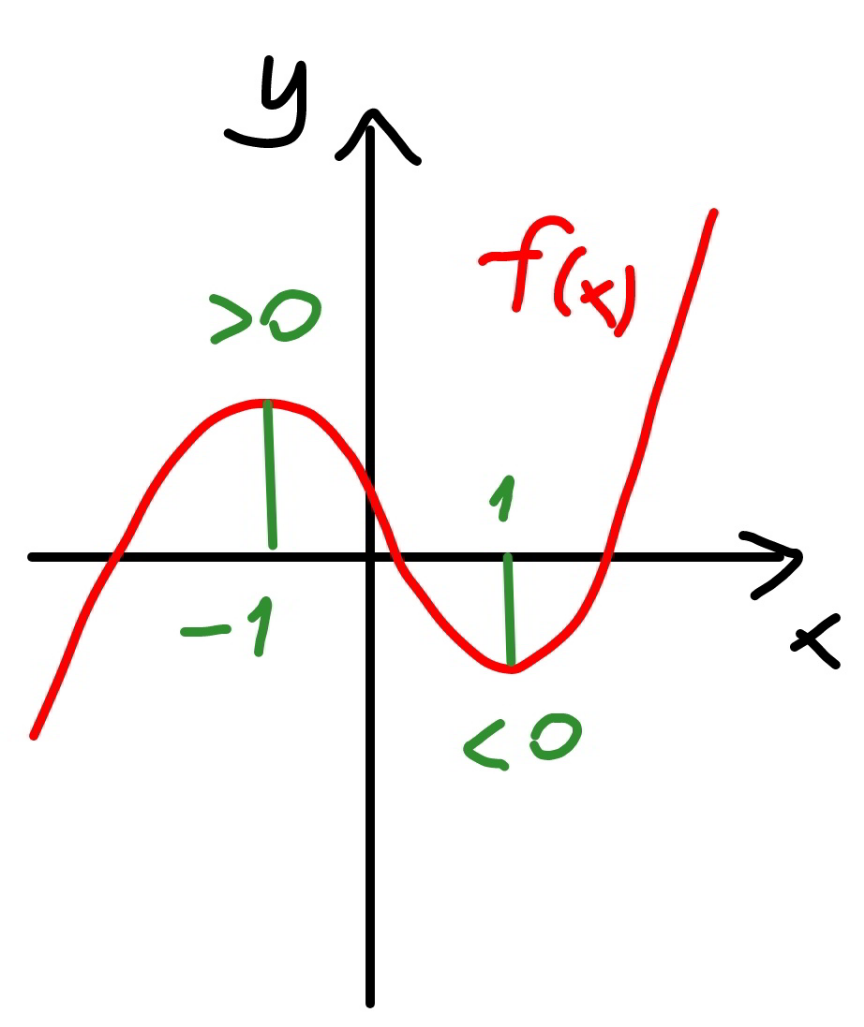
$${f}'\left({x}\right)=\mathrm{99}{x}^{\mathrm{98}} −\mathrm{99}=\mathrm{0} \\ $$$${x}=\pm\mathrm{1} \\ $$$${f}\left(−\mathrm{1}\right)=−\mathrm{1}+\mathrm{99}+\mathrm{1}=\mathrm{99} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}−\mathrm{99}+\mathrm{1}=−\mathrm{97} \\ $$$${f}\left(−\infty\right)\rightarrow−\infty \\ $$$${f}\left(+\infty\right)\rightarrow+\infty \\ $$$$\Rightarrow{three}\:{real}\:{roots}! \\ $$
Commented by mr W last updated on 07/Sep/21