Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 154672 by talminator2856791 last updated on 20/Sep/21

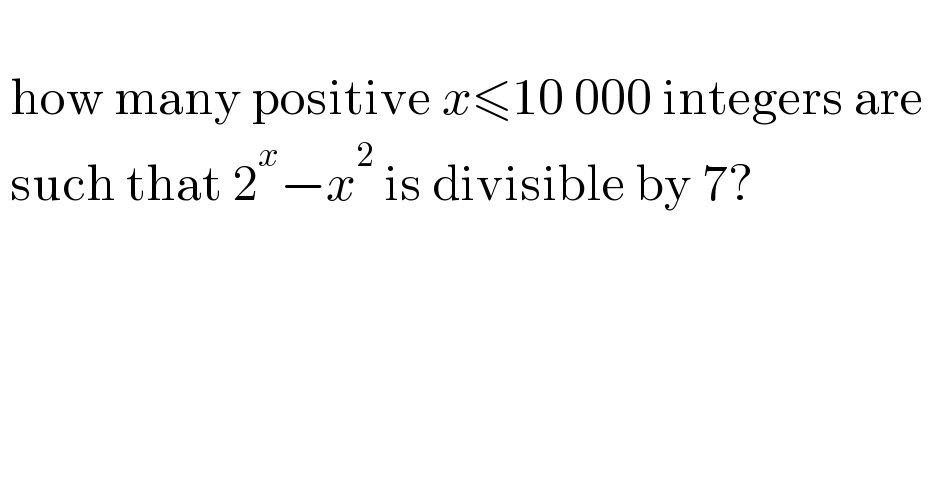
how many positive x≤10 000 integers are such that 2^x −x^2 is divisible by 7?

$$\: \\ $$$$\:\mathrm{how}\:\mathrm{many}\:\mathrm{positive}\:{x}\leqslant\mathrm{10}\:\mathrm{000}\:\mathrm{integers}\:\mathrm{are}\:\: \\ $$$$\:\mathrm{such}\:\mathrm{that}\:\mathrm{2}^{{x}} −{x}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{7}? \\ $$$$\: \\ $$

Answered by MJS_new last updated on 20/Sep/21

2^(3n) =7k+1 2^(3n+1) =7k+2 2^(3n+2) =7k+4 (7n)^2 =7k+0 (7n+1)^2 =7k+1 (7n+2)^2 =7k+4 (7n+3)^2 =7k+2 (7n+4)^2 =7k+2 (7n+5)^2 =7k+4 (7n+6)^2 =7k+1 ⇒ n=0, 1, 2, 3,...: (2^n −n^2 )/7=7k+ 1 1 0 6 0 0 0 2 3 4 0 2 4 1 4 0 5 2 6 5 3 1 1 0 6... ⇒ remainders are 0 for n=21k+{2, 4, 5, 6, 10, 15} 21×476+5=10001 ⇒ ⇒ answer is 475×6+2=2852

$$\mathrm{2}^{\mathrm{3}{n}} =\mathrm{7}{k}+\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} =\mathrm{7}{k}+\mathrm{2} \\ $$$$\mathrm{2}^{\mathrm{3}{n}+\mathrm{2}} =\mathrm{7}{k}+\mathrm{4} \\ $$$$\left(\mathrm{7}{n}\right)^{\mathrm{2}} =\mathrm{7}{k}+\mathrm{0} \\ $$$$\left(\mathrm{7}{n}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{7}{k}+\mathrm{1} \\ $$$$\left(\mathrm{7}{n}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{7}{k}+\mathrm{4} \\ $$$$\left(\mathrm{7}{n}+\mathrm{3}\right)^{\mathrm{2}} =\mathrm{7}{k}+\mathrm{2} \\ $$$$\left(\mathrm{7}{n}+\mathrm{4}\right)^{\mathrm{2}} =\mathrm{7}{k}+\mathrm{2} \\ $$$$\left(\mathrm{7}{n}+\mathrm{5}\right)^{\mathrm{2}} =\mathrm{7}{k}+\mathrm{4} \\ $$$$\left(\mathrm{7}{n}+\mathrm{6}\right)^{\mathrm{2}} =\mathrm{7}{k}+\mathrm{1} \\ $$$$\Rightarrow \\ $$$${n}=\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},...:\:\left(\mathrm{2}^{{n}} −{n}^{\mathrm{2}} \right)/\mathrm{7}=\mathrm{7}{k}+ \\ $$$$\mathrm{1}\:\mathrm{1}\:\mathrm{0}\:\mathrm{6}\:\mathrm{0}\:\mathrm{0}\:\mathrm{0}\:\mathrm{2}\:\mathrm{3}\:\mathrm{4}\:\mathrm{0}\:\mathrm{2}\:\mathrm{4}\:\mathrm{1}\:\mathrm{4}\:\mathrm{0}\:\mathrm{5}\:\mathrm{2}\:\mathrm{6}\:\mathrm{5}\:\mathrm{3}\:\mathrm{1}\:\mathrm{1}\:\mathrm{0}\:\mathrm{6}... \\ $$$$\Rightarrow \\ $$$$\mathrm{remainders}\:\mathrm{are}\:\mathrm{0}\:\mathrm{for} \\ $$$${n}=\mathrm{21}{k}+\left\{\mathrm{2},\:\mathrm{4},\:\mathrm{5},\:\mathrm{6},\:\mathrm{10},\:\mathrm{15}\right\} \\ $$$$\mathrm{21}×\mathrm{476}+\mathrm{5}=\mathrm{10001}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{475}×\mathrm{6}+\mathrm{2}=\mathrm{2852} \\ $$

Commented by mathdanisur last updated on 20/Sep/21

very nice

$$\mathrm{very}\:\mathrm{nice} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com