
Question Number 46760 by arcana last updated on 31/Oct/18

$${how}\:{many}\:{natural}\:{solutions}\:{exist} \\ $$$${to} \\ $$$${x}+{y}+{z}=\mathrm{11},\:{x},{y},{z}\in\mathbb{N} \\ $$
Commented by MrW3 last updated on 31/Oct/18

$${no}.\:{of}\:{ways}\:{to}\:{put}\:\mathrm{11}\:{objects}\:{into}\:\mathrm{3}\:{containers}: \\ $$$${C}_{\mathrm{2}} ^{\mathrm{10}} =\mathrm{45} \\ $$
Answered by Kunal12588 last updated on 31/Oct/18
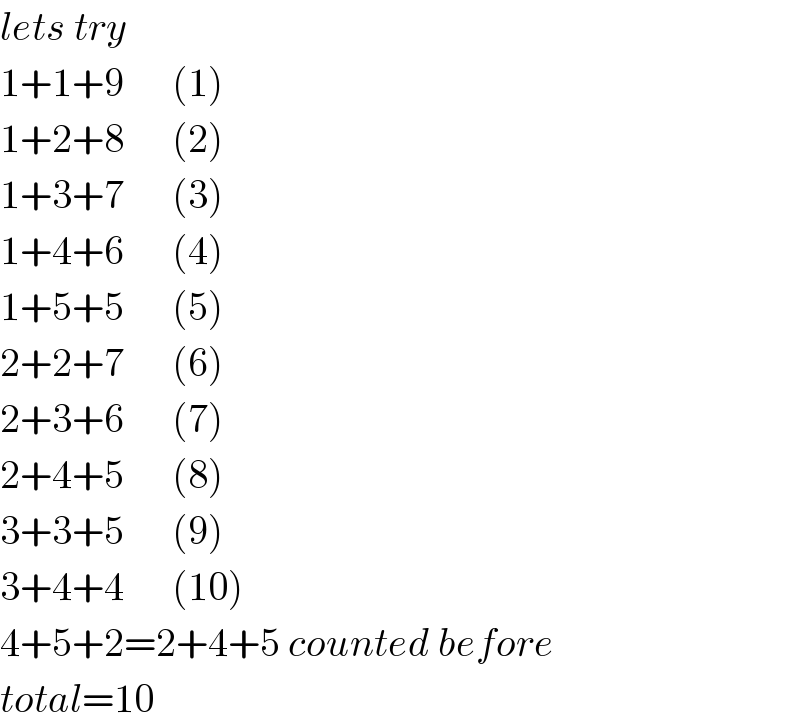
$${lets}\:{try} \\ $$$$\mathrm{1}+\mathrm{1}+\mathrm{9}\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{8}\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\mathrm{1}+\mathrm{3}+\mathrm{7}\:\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$\mathrm{1}+\mathrm{4}+\mathrm{6}\:\:\:\:\:\:\left(\mathrm{4}\right) \\ $$$$\mathrm{1}+\mathrm{5}+\mathrm{5}\:\:\:\:\:\:\left(\mathrm{5}\right) \\ $$$$\mathrm{2}+\mathrm{2}+\mathrm{7}\:\:\:\:\:\:\left(\mathrm{6}\right) \\ $$$$\mathrm{2}+\mathrm{3}+\mathrm{6}\:\:\:\:\:\:\left(\mathrm{7}\right) \\ $$$$\mathrm{2}+\mathrm{4}+\mathrm{5}\:\:\:\:\:\:\left(\mathrm{8}\right) \\ $$$$\mathrm{3}+\mathrm{3}+\mathrm{5}\:\:\:\:\:\:\left(\mathrm{9}\right) \\ $$$$\mathrm{3}+\mathrm{4}+\mathrm{4}\:\:\:\:\:\:\left(\mathrm{10}\right) \\ $$$$\mathrm{4}+\mathrm{5}+\mathrm{2}=\mathrm{2}+\mathrm{4}+\mathrm{5}\:{counted}\:{before} \\ $$$${total}=\mathrm{10} \\ $$
Commented by arcana last updated on 31/Oct/18

$$\mathrm{can}\:\mathrm{you}\:\mathrm{proof}\:\mathrm{it}? \\ $$
Commented by arcana last updated on 31/Oct/18

$${x},{y},{z}\neq\mathrm{0}\:\mathrm{sorry} \\ $$
