Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 218129 by mr W last updated on 30/Mar/25

how many different words can be formed from the word MATHEMATICS? note: here a word should have at least two letters, but mustn′t have a meaning.

$${how}\:{many}\:{different}\:{words}\:{can}\:{be} \\ $$$${formed}\:{from}\:{the}\:{word}\: \\ $$$$\boldsymbol{\mathrm{MATHEMATICS}}? \\ $$$${note}:\:\:{here}\:{a}\:{word}\:{should}\:{have}\:{at}\: \\ $$$${least}\:{two}\:{letters},\:{but}\:{mustn}'{t}\:{have}\:{a} \\ $$$${meaning}. \\ $$

Answered by vnm last updated on 30/Mar/25

Σ_(n=2) ^8 C_8 ^n n!+3Σ_(n=0) ^7 C_7 ^n n!C_(n+2) ^2 + 3Σ_(n=0) ^6 C_6 ^n n!C_(n+4) ^2 C_(n+2) ^2 +Σ_(n=0) ^5 C_5 ^n n!C_(n+6) ^2 C_(n+4) ^2 C_(n+2) ^2 = =13938212 the same result: Σ_(n=2) ^(11) Σ_(k=0) ^(min(3, [(n/2)])) C_(8−k) ^(n−2k) (n−2k)!C_3 ^k Π_(i=0) ^(k−1) C_(n−2i) ^2

$$\underset{{n}=\mathrm{2}} {\overset{\mathrm{8}} {\sum}}{C}_{\mathrm{8}} ^{{n}} {n}!+\mathrm{3}\underset{{n}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}{C}_{\mathrm{7}} ^{{n}} {n}!{C}_{{n}+\mathrm{2}} ^{\mathrm{2}} + \\ $$$$\mathrm{3}\underset{{n}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}{C}_{\mathrm{6}} ^{{n}} {n}!{C}_{{n}+\mathrm{4}} ^{\mathrm{2}} {C}_{{n}+\mathrm{2}} ^{\mathrm{2}} +\underset{{n}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}{C}_{\mathrm{5}} ^{{n}} {n}!{C}_{{n}+\mathrm{6}} ^{\mathrm{2}} {C}_{{n}+\mathrm{4}} ^{\mathrm{2}} {C}_{{n}+\mathrm{2}} ^{\mathrm{2}} = \\ $$$$=\mathrm{13938212} \\ $$$${the}\:{same}\:{result}: \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\mathrm{11}} {\sum}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{min}\left(\mathrm{3},\:\left[\frac{{n}}{\mathrm{2}}\right]\right)} {\sum}}{C}_{\mathrm{8}−{k}} ^{{n}−\mathrm{2}{k}} \left({n}−\mathrm{2}{k}\right)!{C}_{\mathrm{3}} ^{{k}} \underset{{i}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}{C}_{{n}−\mathrm{2}{i}} ^{\mathrm{2}} \\ $$

Commented by mr W last updated on 31/Mar/25

great! thanks sir!

$${great}!\:{thanks}\:{sir}! \\ $$

Answered by mr W last updated on 31/Mar/25

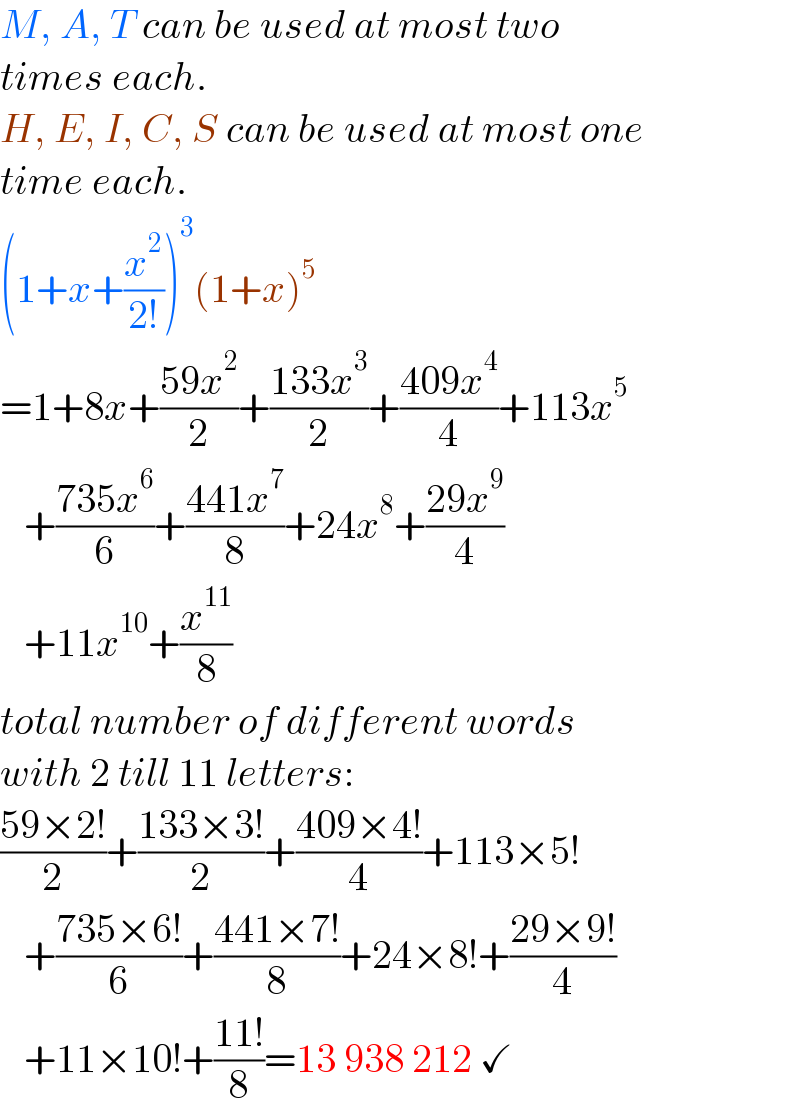
M, A, T can be used at most two times each. H, E, I, C, S can be used at most one time each. (1+x+(x^2 /(2!)))^3 (1+x)^5 =1+8x+((59x^2 )/2)+((133x^3 )/2)+((409x^4 )/4)+113x^5 +((735x^6 )/6)+((441x^7 )/8)+24x^8 +((29x^9 )/4) +11x^(10) +(x^(11) /8) total number of different words with 2 till 11 letters: ((59×2!)/2)+((133×3!)/2)+((409×4!)/4)+113×5! +((735×6!)/6)+((441×7!)/8)+24×8!+((29×9!)/4) +11×10!+((11!)/8)=13 938 212 ✓

$${M},\:{A},\:{T}\:{can}\:{be}\:{used}\:{at}\:{most}\:{two}\: \\ $$$${times}\:{each}. \\ $$$${H},\:{E},\:{I},\:{C},\:{S}\:{can}\:{be}\:{used}\:{at}\:{most}\:{one} \\ $$$${time}\:{each}. \\ $$$$\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}\right)^{\mathrm{3}} \left(\mathrm{1}+{x}\right)^{\mathrm{5}} \\ $$$$=\mathrm{1}+\mathrm{8}{x}+\frac{\mathrm{59}{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{133}{x}^{\mathrm{3}} }{\mathrm{2}}+\frac{\mathrm{409}{x}^{\mathrm{4}} }{\mathrm{4}}+\mathrm{113}{x}^{\mathrm{5}} \\ $$$$\:\:\:+\frac{\mathrm{735}{x}^{\mathrm{6}} }{\mathrm{6}}+\frac{\mathrm{441}{x}^{\mathrm{7}} }{\mathrm{8}}+\mathrm{24}{x}^{\mathrm{8}} +\frac{\mathrm{29}{x}^{\mathrm{9}} }{\mathrm{4}} \\ $$$$\:\:\:+\mathrm{11}{x}^{\mathrm{10}} +\frac{{x}^{\mathrm{11}} }{\mathrm{8}} \\ $$$${total}\:{number}\:{of}\:{different}\:{words}\: \\ $$$${with}\:\mathrm{2}\:{till}\:\mathrm{11}\:{letters}: \\ $$$$\frac{\mathrm{59}×\mathrm{2}!}{\mathrm{2}}+\frac{\mathrm{133}×\mathrm{3}!}{\mathrm{2}}+\frac{\mathrm{409}×\mathrm{4}!}{\mathrm{4}}+\mathrm{113}×\mathrm{5}! \\ $$$$\:\:\:+\frac{\mathrm{735}×\mathrm{6}!}{\mathrm{6}}+\frac{\mathrm{441}×\mathrm{7}!}{\mathrm{8}}+\mathrm{24}×\mathrm{8}!+\frac{\mathrm{29}×\mathrm{9}!}{\mathrm{4}} \\ $$$$\:\:\:+\mathrm{11}×\mathrm{10}!+\frac{\mathrm{11}!}{\mathrm{8}}=\mathrm{13}\:\mathrm{938}\:\mathrm{212}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com