
Question Number 187916 by mustafazaheen last updated on 23/Feb/23
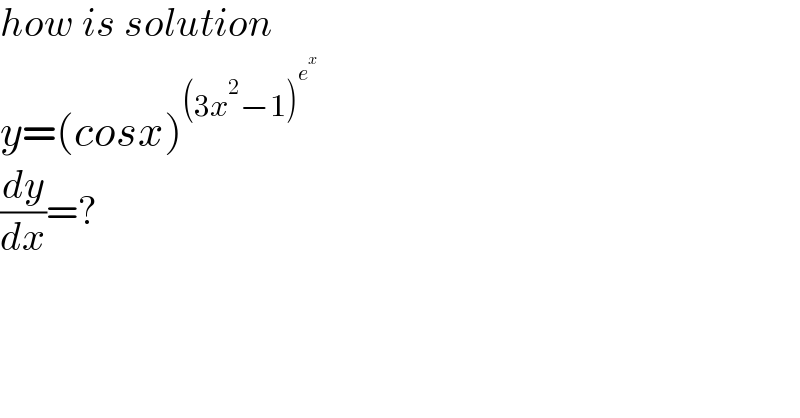
$${how}\:{is}\:{solution} \\ $$$${y}=\left({cosx}\right)^{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } } \\ $$$$\frac{{dy}}{{dx}}=? \\ $$
Answered by mr W last updated on 23/Feb/23
![generally y=f(x)^(g(x)) =e^(g(x)ln f(x)) y′=f(x)^(g(x)) [g′(x)ln f(x)+((g(x)f′(x))/(f(x)))] y=(cos x)^((3x^2 −1)^e^x ) y′=(cos x)^((3x^2 −1)^e^x ) {[(3x^2 −1)^e^x ]^, ln (cos x)−(((3x^2 −1)^e^x sin x)/(cos x))} =(cos x)^((3x^2 −1)^e^x ) {[(3x^2 −1)^e^x (e^x ln (3x^2 −1)+((6xe^x )/(3x^2 −1)))]ln (cos x)−(((3x^2 −1)^e^x sin x)/(cos x))} =(cos x)^((3x^2 −1)^e^x ) {[(3x^2 −1)^e^x e^x (ln (3x^2 −1)+((6x)/(3x^2 −1)))]ln (cos x)−(((3x^2 −1)^e^x sin x)/(cos x))}](Q187937.png)
$${generally} \\ $$$${y}={f}\left({x}\right)^{{g}\left({x}\right)} ={e}^{{g}\left({x}\right)\mathrm{ln}\:{f}\left({x}\right)} \\ $$$${y}'={f}\left({x}\right)^{{g}\left({x}\right)} \left[{g}'\left({x}\right)\mathrm{ln}\:{f}\left({x}\right)+\frac{{g}\left({x}\right){f}'\left({x}\right)}{{f}\left({x}\right)}\right] \\ $$$$ \\ $$$${y}=\left(\mathrm{cos}\:{x}\right)^{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } } \\ $$$${y}'=\left(\mathrm{cos}\:{x}\right)^{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } } \left\{\left[\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } \right]^{,} \mathrm{ln}\:\left(\mathrm{cos}\:{x}\right)−\frac{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } \mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\right\} \\ $$$$\:\:=\left(\mathrm{cos}\:{x}\right)^{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } } \left\{\left[\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } \left({e}^{{x}} \mathrm{ln}\:\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)+\frac{\mathrm{6}{xe}^{{x}} }{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}}\right)\right]\mathrm{ln}\:\left(\mathrm{cos}\:{x}\right)−\frac{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } \mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\right\} \\ $$$$\:\:=\left(\mathrm{cos}\:{x}\right)^{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } } \left\{\left[\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } {e}^{{x}} \left(\mathrm{ln}\:\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)+\frac{\mathrm{6}{x}}{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}}\right)\right]\mathrm{ln}\:\left(\mathrm{cos}\:{x}\right)−\frac{\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{e}^{{x}} } \mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\right\} \\ $$
Commented by mustafazaheen last updated on 23/Feb/23

$${Thanks}\:{Mr} \\ $$
