
Question Number 76232 by Rio Michael last updated on 25/Dec/19
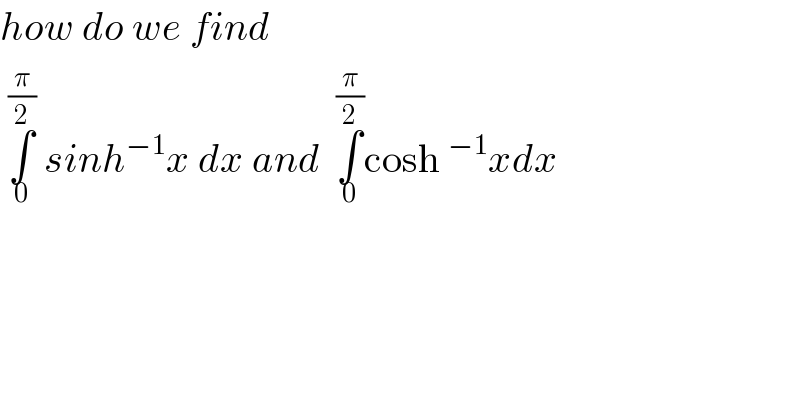
$${how}\:{do}\:{we}\:{find} \\ $$$$\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:{sinh}^{−\mathrm{1}} {x}\:{dx}\:{and}\:\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{cosh}\:^{−\mathrm{1}} {xdx} \\ $$
Commented by mr W last updated on 25/Dec/19
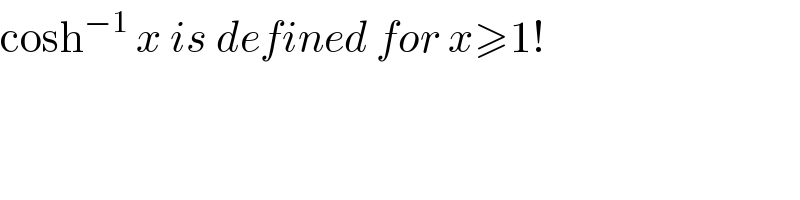
$$\mathrm{cosh}^{−\mathrm{1}} \:{x}\:{is}\:{defined}\:{for}\:{x}\geqslant\mathrm{1}! \\ $$
Commented by turbo msup by abdo last updated on 25/Dec/19
![let I =∫_0 ^(π/2) argsh(x)dx ⇒I =_(argsh(x)=t) ∫_0 ^(argsh((π/2))) t ch(t)dt =∫_0 ^(ln((π/2)+(√(1+(π^2 /4))))) tcht()dt =_(by parts) [tsh(t)]_0 ^(ln((π/2)+(√(1+(π^2 /4))))) −∫_0 ^(ln((π/2)+(√(1+(π^2 /4))))) sh(t)dt =ln((π/2)+(√(1+(π^2 /4))))(((π/2)+(√(1+(π^2 /4)))−((π/2)+(√(1+(π^2 /4))))^(−1) )/2) −(1/2)((π/2)+(√(1+(π^2 /4))))+((π/2)+(√(1+(π^2 /4))))^(−1) )](Q76262.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{argsh}\left({x}\right){dx} \\ $$$$\Rightarrow{I}\:=_{{argsh}\left({x}\right)={t}} \:\:\:\int_{\mathrm{0}} ^{{argsh}\left(\frac{\pi}{\mathrm{2}}\right)} {t}\:{ch}\left({t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{{ln}\left(\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}\right)} \:{tcht}\left(\right){dt} \\ $$$$=_{{by}\:{parts}} \:\:\left[{tsh}\left({t}\right)\right]_{\mathrm{0}} ^{{ln}\left(\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}\right)} \\ $$$$−\int_{\mathrm{0}} ^{{ln}\left(\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}\right)} {sh}\left({t}\right){dt} \\ $$$$={ln}\left(\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}\right)\frac{\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}−\left(\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}\right)^{−\mathrm{1}} }{\mathrm{2}} \\ $$$$\left.−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}\right)+\left(\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}\right)^{−\mathrm{1}} \right) \\ $$$$ \\ $$
Answered by mind is power last updated on 25/Dec/19
![u=sh^− (x) by part ∫sh^− (x)dx=[xsh^− (x)]−∫(x/(√(1+x^2 )))dx =xsh^− (x)−(√(x^2 +1))+c sam with ch^− (x)](Q76235.png)
$$\mathrm{u}=\mathrm{sh}^{−} \left(\mathrm{x}\right) \\ $$$$\mathrm{by}\:\mathrm{part} \\ $$$$\int\mathrm{sh}^{−} \left(\mathrm{x}\right)\mathrm{dx}=\left[\mathrm{xsh}^{−} \left(\mathrm{x}\right)\right]−\int\frac{\mathrm{x}}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mathrm{dx} \\ $$$$=\mathrm{xsh}^{−} \left(\mathrm{x}\right)−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{c} \\ $$$$\mathrm{sam}\:\mathrm{with}\:\mathrm{ch}^{−} \left(\mathrm{x}\right) \\ $$
Answered by mr W last updated on 25/Dec/19
![∫_0 ^(π/2) sinh^(−1) x dx =(π/2)sinh^(−1) ((π/2))−∫_0 ^(sinh^(−1) ((π/2))) sinh y dy =(π/2)sinh^(−1) ((π/2))−[cosh (sinh^(−1) (π/2))−1] =(π/2)ln ((π/2)+(√(1+((π/2))^2 )))+1−(√(1+((π/2))^2 )) ≈1.075329](Q76237.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sinh}^{−\mathrm{1}} \:{x}\:{dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\pi}{\mathrm{2}}\right)−\int_{\mathrm{0}} ^{\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\pi}{\mathrm{2}}\right)} \mathrm{sinh}\:{y}\:{dy} \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\pi}{\mathrm{2}}\right)−\left[\mathrm{cosh}\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\frac{\pi}{\mathrm{2}}\right)−\mathrm{1}\right] \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{ln}\:\left(\frac{\pi}{\mathrm{2}}+\sqrt{\mathrm{1}+\left(\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} }\right)+\mathrm{1}−\sqrt{\mathrm{1}+\left(\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\approx\mathrm{1}.\mathrm{075329} \\ $$
Commented by mr W last updated on 25/Dec/19
Commented by mr W last updated on 25/Dec/19
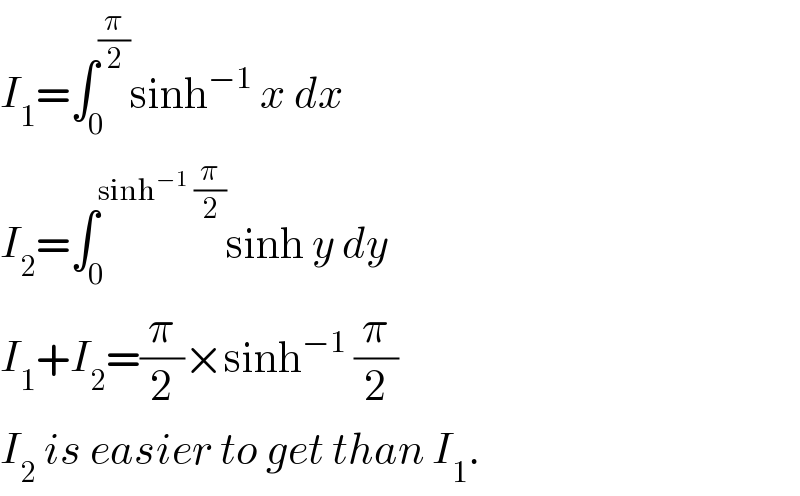
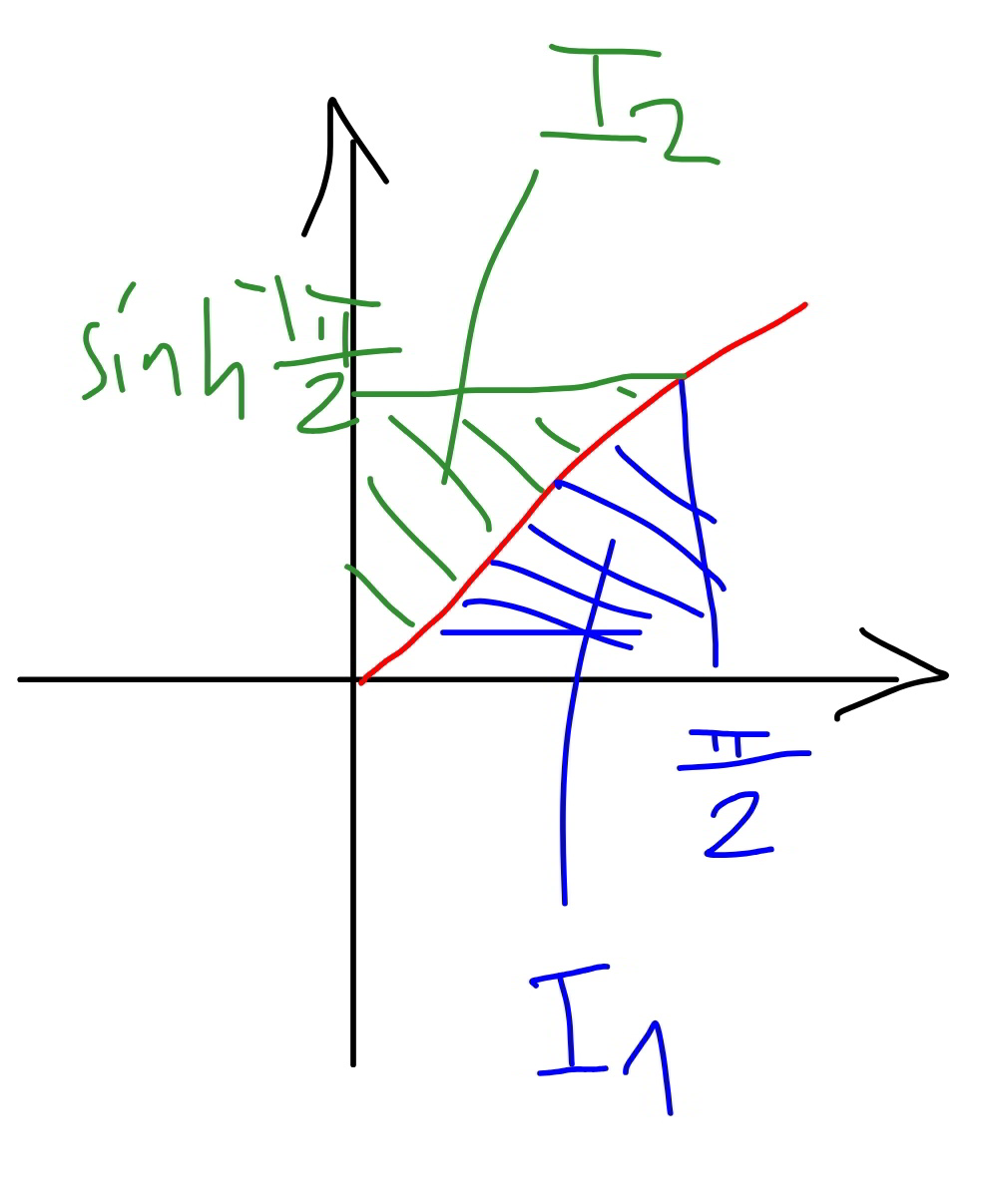
$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sinh}^{−\mathrm{1}} \:{x}\:{dx} \\ $$$${I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{sinh}^{−\mathrm{1}} \:\frac{\pi}{\mathrm{2}}} \mathrm{sinh}\:{y}\:{dy} \\ $$$${I}_{\mathrm{1}} +{I}_{\mathrm{2}} =\frac{\pi}{\mathrm{2}}×\mathrm{sinh}^{−\mathrm{1}} \:\frac{\pi}{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} \:{is}\:{easier}\:{to}\:{get}\:{than}\:{I}_{\mathrm{1}} . \\ $$
Commented by Rio Michael last updated on 25/Dec/19

$${thanks} \\ $$
Commented by mr W last updated on 25/Dec/19
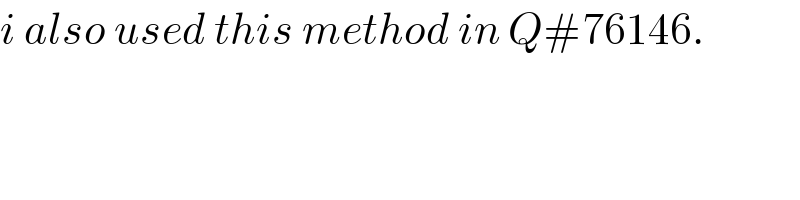
$${i}\:{also}\:{used}\:{this}\:{method}\:{in}\:{Q}#\mathrm{76146}. \\ $$
