
Question Number 133734 by Abdoulaye last updated on 23/Feb/21

$${how}\:{do}\:{we}\:{caculate}\:\int{ln}\left({tanx}\right){dx}\:? \\ $$
Answered by mathmax by abdo last updated on 24/Feb/21
![f(x)=∫_(π/4) ^x ln(tanx)dx ⇒f(x)=_(tanx=t) ∫_1 ^(tanx) ((ln(t))/(1+t^2 ))dt =[arctan(t)ln(t)]_1 ^(tanx) −∫_1 ^(tanx) ((arctant)/t)dt =xln(tanx)−∫_1 ^(tanx) ((arctan(t))/t)dt we have (arctant)^((1)) =(1/(1+t^2 )) =Σ_(n=0) ^∞ (−1)^n t^(2n) ⇒arctan(t)=Σ_(n=0) ^∞ (((−1)^n )/(2n+1))t^(2n+1) +c(c=0) ⇒ ((arctant)/t)=Σ_(n=0) ^∞ (((−1)^n )/(2n+1))t^(2n) ⇒f(x)=xln(x)−∫_1 ^(tanx) Σ_(n=0) ^∞ (((−1)^n )/(2n+1))t^(2n) dt =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))[(1/(2n+1))t^(2n+1) ]_1 ^(tanx) =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))(tan^(2n+1) x−1) =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))tan^(2n+1) x−K (katalan constant)....be continued...](Q133750.png)
$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{x}} \mathrm{ln}\left(\mathrm{tanx}\right)\mathrm{dx}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=_{\mathrm{tanx}=\mathrm{t}} \:\:\:\int_{\mathrm{1}} ^{\mathrm{tanx}} \frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\left[\mathrm{arctan}\left(\mathrm{t}\right)\mathrm{ln}\left(\mathrm{t}\right)\right]_{\mathrm{1}} ^{\mathrm{tanx}} −\int_{\mathrm{1}} ^{\mathrm{tanx}} \frac{\mathrm{arctant}}{\mathrm{t}}\mathrm{dt} \\ $$$$=\mathrm{xln}\left(\mathrm{tanx}\right)−\int_{\mathrm{1}} ^{\mathrm{tanx}} \:\frac{\mathrm{arctan}\left(\mathrm{t}\right)}{\mathrm{t}}\mathrm{dt}\:\mathrm{we}\:\mathrm{have}\:\left(\mathrm{arctant}\right)^{\left(\mathrm{1}\right)} =\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{t}^{\mathrm{2n}} \:\Rightarrow\mathrm{arctan}\left(\mathrm{t}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\mathrm{t}^{\mathrm{2n}+\mathrm{1}} +\mathrm{c}\left(\mathrm{c}=\mathrm{0}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{arctant}}{\mathrm{t}}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\mathrm{t}^{\mathrm{2n}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{xln}\left(\mathrm{x}\right)−\int_{\mathrm{1}} ^{\mathrm{tanx}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\mathrm{t}^{\mathrm{2n}} \mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\left[\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{t}^{\mathrm{2n}+\mathrm{1}} \right]_{\mathrm{1}} ^{\mathrm{tanx}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{tan}^{\mathrm{2n}+\mathrm{1}} \mathrm{x}−\mathrm{1}\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{tan}^{\mathrm{2n}+\mathrm{1}} \mathrm{x}−\mathrm{K}\:\:\left(\mathrm{katalan}\:\mathrm{constant}\right)....\mathrm{be}\:\mathrm{continued}... \\ $$
Commented by Abdoulaye last updated on 24/Feb/21

$${thank} \\ $$$${please}\:{what}\:\:{katalan}\:{canstant}? \\ $$
Commented by Dwaipayan Shikari last updated on 24/Feb/21
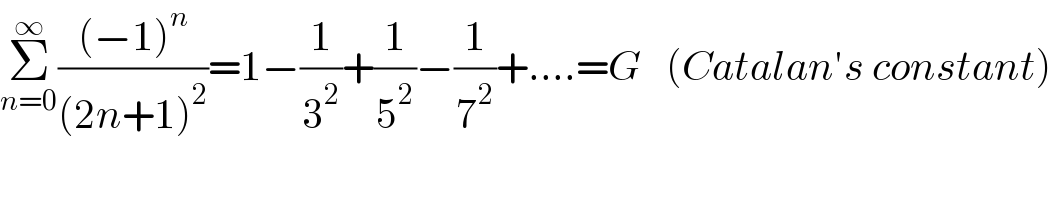
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }+....={G}\:\:\:\left({Catalan}'{s}\:{constant}\right) \\ $$
