
Question Number 197275 by uchihayahia last updated on 12/Sep/23
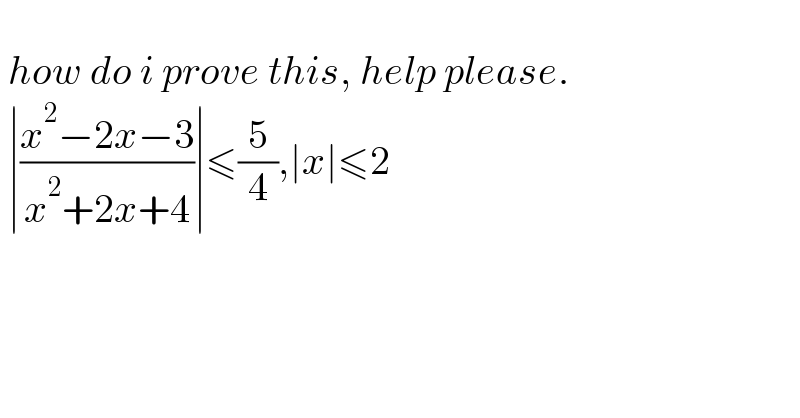
$$ \\ $$$$\:{how}\:{do}\:{i}\:{prove}\:{this},\:{help}\:{please}. \\ $$$$\:\mid\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}\mid\leqslant\frac{\mathrm{5}}{\mathrm{3}},\mid{x}\mid\leqslant\mathrm{2} \\ $$$$ \\ $$$$ \\ $$
Answered by AST last updated on 12/Sep/23
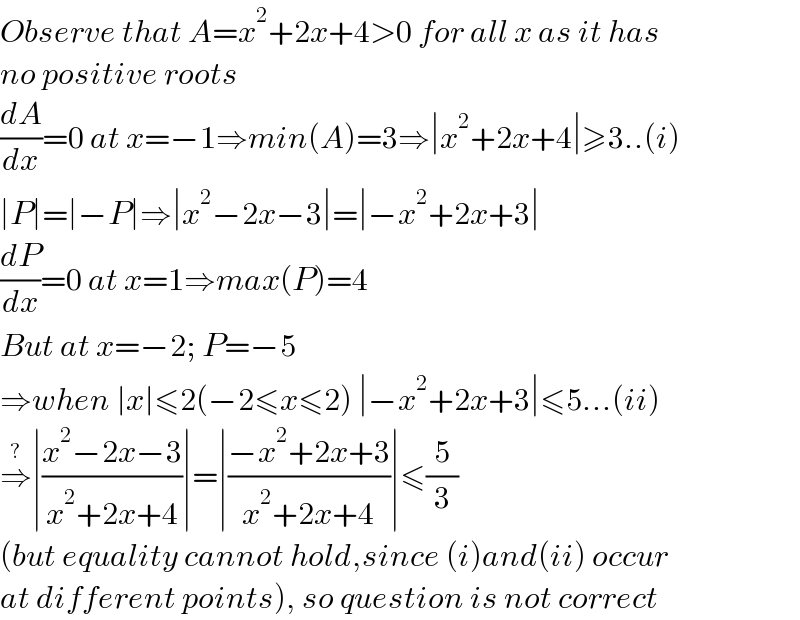
$${Observe}\:{that}\:{A}={x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}>\mathrm{0}\:{for}\:{all}\:{x}\:{as}\:{it}\:{has} \\ $$$${no}\:{positive}\:{roots} \\ $$$$\frac{{dA}}{{dx}}=\mathrm{0}\:{at}\:{x}=−\mathrm{1}\Rightarrow{min}\left({A}\right)=\mathrm{3}\Rightarrow\mid{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\mid\geqslant\mathrm{3}..\left({i}\right) \\ $$$$\mid{P}\mid=\mid−{P}\mid\Rightarrow\mid{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}\mid=\mid−{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\mid \\ $$$$\frac{{dP}}{{dx}}=\mathrm{0}\:{at}\:{x}=\mathrm{1}\Rightarrow{max}\left({P}\right)=\mathrm{4} \\ $$$${But}\:{at}\:{x}=−\mathrm{2};\:{P}=−\mathrm{5} \\ $$$$\Rightarrow{when}\:\mid{x}\mid\leqslant\mathrm{2}\left(−\mathrm{2}\leqslant{x}\leqslant\mathrm{2}\right)\:\mid−{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\mid\leqslant\mathrm{5}...\left({ii}\right) \\ $$$$\overset{?} {\Rightarrow}\mid\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}\mid=\mid\frac{−{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}\mid\leqslant\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\left({but}\:{equality}\:{cannot}\:{hold},{since}\:\left({i}\right){and}\left({ii}\right)\:{occur}\right. \\ $$$$\left.{at}\:{different}\:{points}\right),\:{so}\:{question}\:{is}\:{not}\:{correct} \\ $$
Commented by AST last updated on 12/Sep/23

Commented by uchihayahia last updated on 13/Sep/23

$${i}'{m}\:{sorry},\:{but}\:{i}\:{checked}\:{geogebra} \\ $$$$\:{and}\:{the}\:{the}\:{statement}\:{is}\:{true} \\ $$
Commented by AST last updated on 13/Sep/23
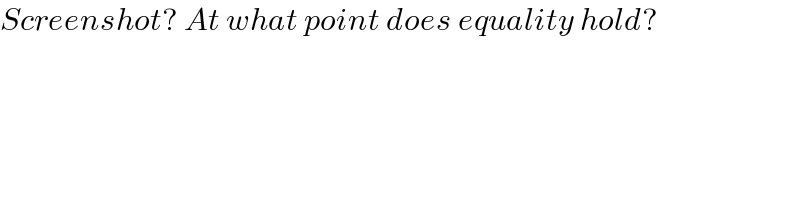
$${Screenshot}?\:{At}\:{what}\:{point}\:{does}\:{equality}\:{hold}? \\ $$
Commented by uchihayahia last updated on 13/Sep/23

$$ \\ $$
Commented by uchihayahia last updated on 13/Sep/23
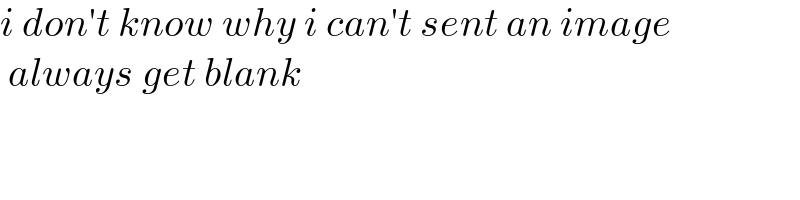
$${i}\:{don}'{t}\:{know}\:{why}\:{i}\:{can}'{t}\:{sent}\:{an}\:{image} \\ $$$$\:{always}\:{get}\:{blank} \\ $$
Commented by AST last updated on 13/Sep/23
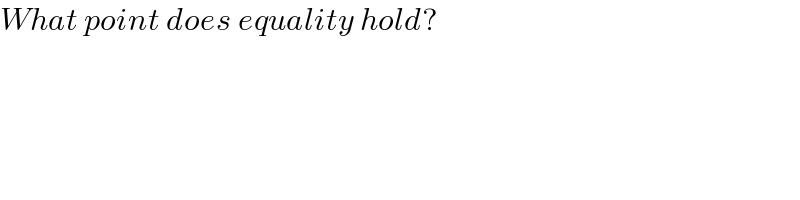
$${What}\:{point}\:{does}\:{equality}\:{hold}? \\ $$
Commented by uchihayahia last updated on 13/Sep/23
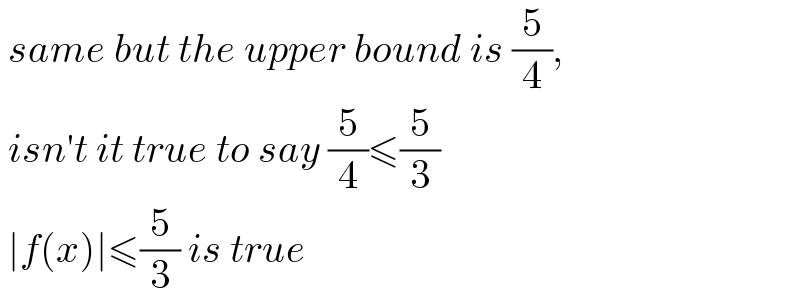
$$\:{same}\:{but}\:{the}\:{upper}\:{bound}\:{is}\:\frac{\mathrm{5}}{\mathrm{4}}, \\ $$$$\:{isn}'{t}\:{it}\:{true}\:{to}\:{say}\:\frac{\mathrm{5}}{\mathrm{4}}\leqslant\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\:\mid{f}\left({x}\right)\mid\leqslant\frac{\mathrm{5}}{\mathrm{3}}\:{is}\:{true} \\ $$
Commented by AST last updated on 13/Sep/23
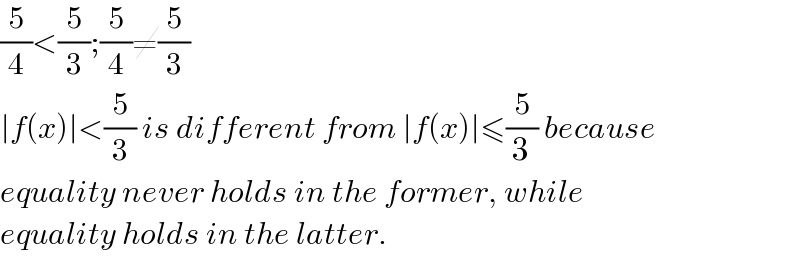
$$\frac{\mathrm{5}}{\mathrm{4}}<\frac{\mathrm{5}}{\mathrm{3}};\frac{\mathrm{5}}{\mathrm{4}}\neq\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mid{f}\left({x}\right)\mid<\frac{\mathrm{5}}{\mathrm{3}}\:{is}\:{different}\:{from}\:\mid{f}\left({x}\right)\mid\leqslant\frac{\mathrm{5}}{\mathrm{3}}\:{because} \\ $$$${equality}\:{never}\:{holds}\:{in}\:{the}\:{former},\:{while}\: \\ $$$${equality}\:{holds}\:{in}\:{the}\:{latter}. \\ $$
