Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 76053 by john santuy last updated on 23/Dec/19

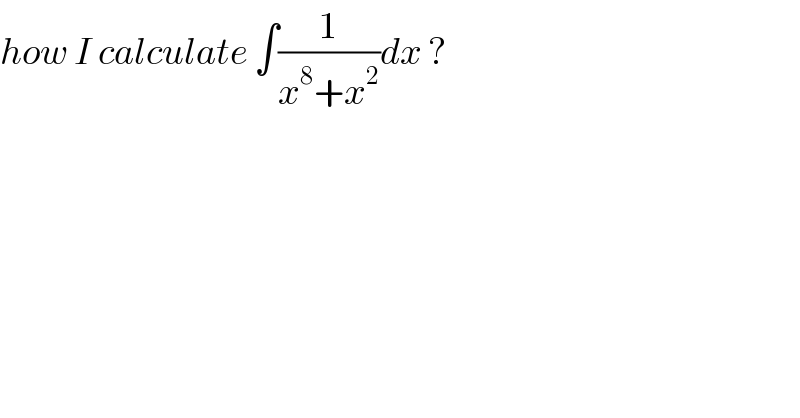
how I calculate ∫(1/(x^8 +x^2 ))dx ?

$${how}\:{I}\:{calculate}\:\int\frac{\mathrm{1}}{{x}^{\mathrm{8}} +{x}^{\mathrm{2}} }{dx}\:? \\ $$

Commented by abdomathmax last updated on 23/Dec/19

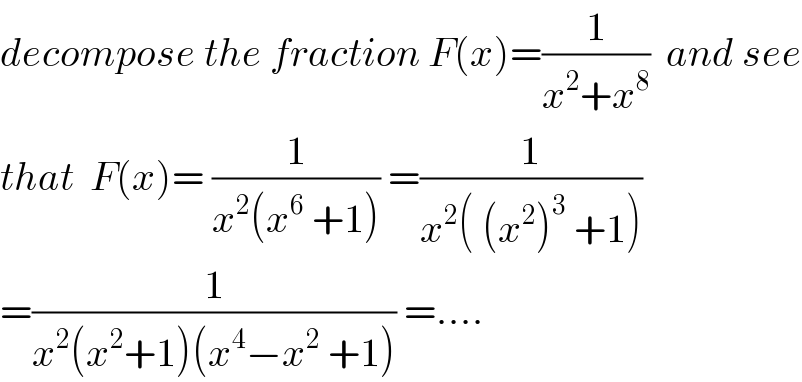
decompose the fraction F(x)=(1/(x^2 +x^8 )) and see that F(x)= (1/(x^2 (x^6 +1))) =(1/(x^2 ( (x^2 )^3 +1))) =(1/(x^2 (x^2 +1)(x^4 −x^2 +1))) =....

$${decompose}\:{the}\:{fraction}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}^{\mathrm{8}} }\:\:{and}\:{see} \\ $$$${that}\:\:{F}\left({x}\right)=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{6}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(\:\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} \:+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=.... \\ $$

Commented by benjo last updated on 23/Dec/19

thanks sir

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Answered by MJS last updated on 23/Dec/19

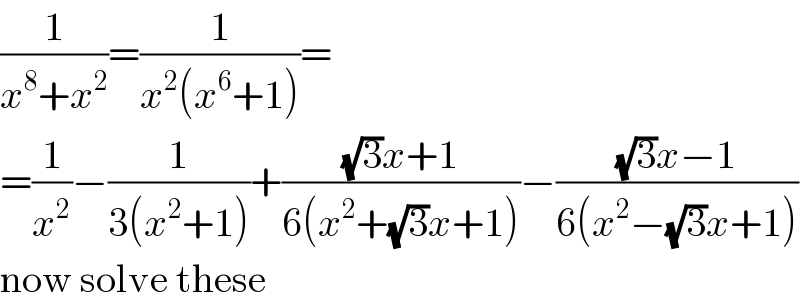
(1/(x^8 +x^2 ))=(1/(x^2 (x^6 +1)))= =(1/x^2 )−(1/(3(x^2 +1)))+(((√3)x+1)/(6(x^2 +(√3)x+1)))−(((√3)x−1)/(6(x^2 −(√3)x+1))) now solve these

$$\frac{\mathrm{1}}{{x}^{\mathrm{8}} +{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{6}} +\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\sqrt{\mathrm{3}}{x}+\mathrm{1}}{\mathrm{6}\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)}−\frac{\sqrt{\mathrm{3}}{x}−\mathrm{1}}{\mathrm{6}\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)} \\ $$$$\mathrm{now}\:\mathrm{solve}\:\mathrm{these} \\ $$

Commented by benjo last updated on 23/Dec/19

thanks sir]

$$\left.\mathrm{thanks}\:\mathrm{sir}\right] \\ $$

Commented by vishalbhardwaj last updated on 23/Dec/19

sir this procedure is very difficult to undersatand , please explain this once again when you are direct ly taken any value of x

$$\mathrm{sir}\:\mathrm{this}\:\mathrm{procedure}\:\mathrm{is}\:\mathrm{very}\:\mathrm{difficult}\:\mathrm{to}\:\mathrm{undersatand} \\ $$$$,\:\mathrm{please}\:\mathrm{explain}\:\mathrm{this}\:\mathrm{once}\:\mathrm{again}\:\mathrm{when}\:\mathrm{you}\:\mathrm{are}\:\mathrm{direct} \\ $$$$\mathrm{ly}\:\mathrm{taken}\:\mathrm{any}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x} \\ $$$$ \\ $$

Commented by MJS last updated on 23/Dec/19

the decomposing or the integration?

$$\mathrm{the}\:\mathrm{decomposing}\:\mathrm{or}\:\mathrm{the}\:\mathrm{integration}? \\ $$

Commented by vishalbhardwaj last updated on 23/Dec/19

decomposing

$$\mathrm{decomposing} \\ $$

Commented by MJS last updated on 24/Dec/19

x^8 +x^2 =x^2 (x^6 +1)= =x^2 ((x^2 )^3 +1)= [((p^3 +1=(p+1)(p^2 −p+1))) ] =x^2 (x^2 +1)(x^4 −x^2 +1)= [((x^4 −x^2 +1=0 let x=(√q))),((q^2 −q+1=0 ⇒ q=−(1/2)±((√3)/2)i)),((these are the 2^(nd) and 3^(rd) solutions)),((of q^3 +1=0 ⇒ q=e^(±i(π/3)) )),((⇒ x=e^(±i(π/6)) ∨x=e^(±i((5π)/6)) )),((⇒ x^4 −x^2 +1=)),((=(x−e^(−i(π/6)) )(x−e^(i(π/6)) )(x−e^(−i((5π)/6)) )(x−e^(i((5π)/6)) )=)),((=(x^2 −(√3)x+1)(x^2 +(√3)x+1))) ] =x^2 (x^2 +1)(x^2 −(√3)x+1)(x^2 +(√3)x+1) ⇒ (1/(x^8 +x^2 ))=((ax+b)/x^2 )+((cx+d)/(x^2 +1))+((ex+f)/(x^2 −(√3)x+1))+((gx+h)/(x^2 +(√3)x+1)) now use your (hopefully) learned method

$${x}^{\mathrm{8}} +{x}^{\mathrm{2}} ={x}^{\mathrm{2}} \left({x}^{\mathrm{6}} +\mathrm{1}\right)= \\ $$$$={x}^{\mathrm{2}} \left(\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} +\mathrm{1}\right)= \\ $$$$\:\:\:\:\:\begin{bmatrix}{{p}^{\mathrm{3}} +\mathrm{1}=\left({p}+\mathrm{1}\right)\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right)}\end{bmatrix} \\ $$$$={x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)= \\ $$$$\:\:\:\:\:\begin{bmatrix}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:\mathrm{let}\:{x}=\sqrt{{q}}}\\{{q}^{\mathrm{2}} −{q}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:{q}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}}\\{\mathrm{these}\:\mathrm{are}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{and}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{solutions}}\\{\mathrm{of}\:{q}^{\mathrm{3}} +\mathrm{1}=\mathrm{0}\:\Rightarrow\:{q}=\mathrm{e}^{\pm\mathrm{i}\frac{\pi}{\mathrm{3}}} }\\{\Rightarrow\:{x}=\mathrm{e}^{\pm\mathrm{i}\frac{\pi}{\mathrm{6}}} \vee{x}=\mathrm{e}^{\pm\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{6}}} }\\{\Rightarrow\:{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}=}\\{=\left({x}−\mathrm{e}^{−\mathrm{i}\frac{\pi}{\mathrm{6}}} \right)\left({x}−\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{6}}} \right)\left({x}−\mathrm{e}^{−\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{6}}} \right)\left({x}−\mathrm{e}^{\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{6}}} \right)=}\\{=\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)}\end{bmatrix} \\ $$$$={x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right) \\ $$$$\Rightarrow \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{8}} +{x}^{\mathrm{2}} }=\frac{{ax}+{b}}{{x}^{\mathrm{2}} }+\frac{{cx}+{d}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{{ex}+{f}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}+\frac{{gx}+{h}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{your}\:\left(\mathrm{hopefully}\right)\:\mathrm{learned}\:\mathrm{method} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com