
Question Number 133653 by greg_ed last updated on 23/Feb/21

$$\boldsymbol{\mathrm{hi}},\:\boldsymbol{\mathrm{everybody}}\:! \\ $$$$\boldsymbol{\mathrm{how}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\pi}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{an}}\:\boldsymbol{\mathrm{irrational}}\:\boldsymbol{\mathrm{number}}\:??? \\ $$
Answered by Dwaipayan Shikari last updated on 23/Feb/21
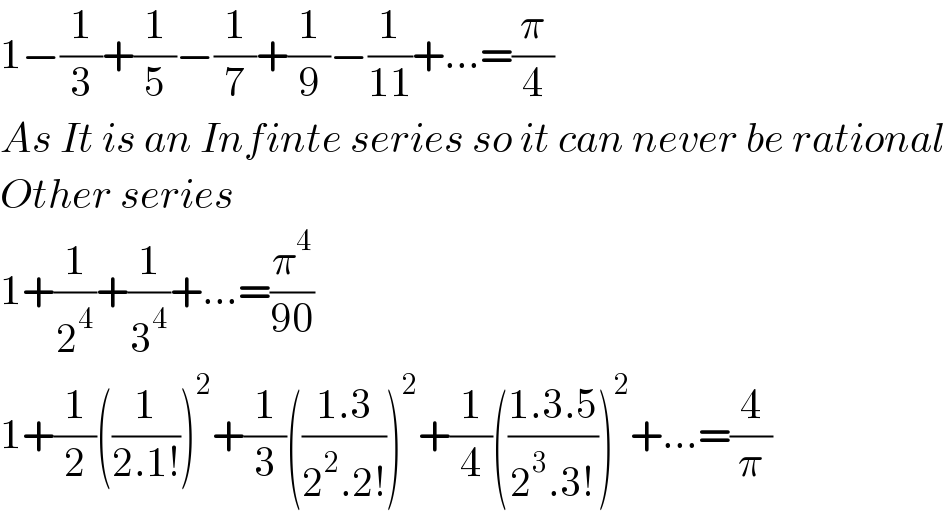
$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{11}}+...=\frac{\pi}{\mathrm{4}} \\ $$$${As}\:{It}\:{is}\:{an}\:{Infinte}\:{series}\:{so}\:{it}\:{can}\:{never}\:{be}\:{rational} \\ $$$${Other}\:{series} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }+...=\frac{\pi^{\mathrm{4}} }{\mathrm{90}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}.\mathrm{1}!}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}.\mathrm{3}}{\mathrm{2}^{\mathrm{2}} .\mathrm{2}!}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}}{\mathrm{2}^{\mathrm{3}} .\mathrm{3}!}\right)^{\mathrm{2}} +...=\frac{\mathrm{4}}{\pi} \\ $$
