
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 163283 by greg_ed last updated on 05/Jan/22

$$\mathrm{hi}\:! \\ $$We store 5 objects in three discernible drawers. Suppose that the different ways of carrying out these arrangements are equally probable, calculate the probability that one of the 3 drawers contains at least 3 objects.
Commented by mr W last updated on 05/Jan/22
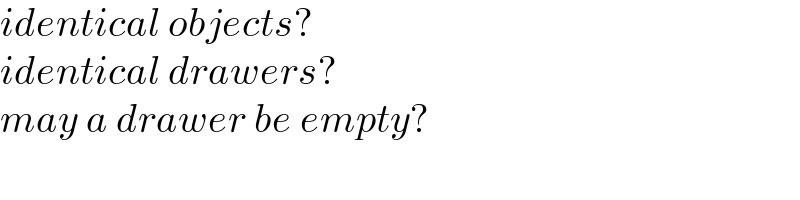
$${identical}\:{objects}? \\ $$$${identical}\:{drawers}? \\ $$$${may}\:{a}\:{drawer}\:{be}\:{empty}? \\ $$
Answered by mr W last updated on 06/Jan/22
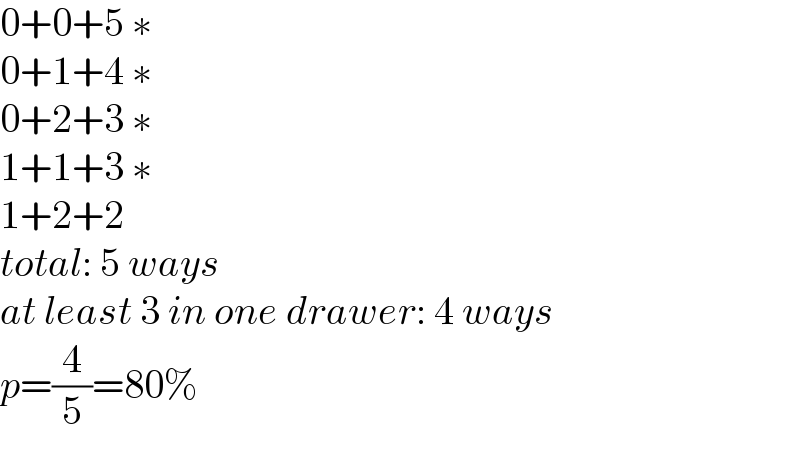
$$\mathrm{0}+\mathrm{0}+\mathrm{5}\:\ast \\ $$$$\mathrm{0}+\mathrm{1}+\mathrm{4}\:\ast \\ $$$$\mathrm{0}+\mathrm{2}+\mathrm{3}\:\ast \\ $$$$\mathrm{1}+\mathrm{1}+\mathrm{3}\:\ast \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{2} \\ $$$${total}:\:\mathrm{5}\:{ways} \\ $$$${at}\:{least}\:\mathrm{3}\:{in}\:{one}\:{drawer}:\:\mathrm{4}\:{ways} \\ $$$${p}=\frac{\mathrm{4}}{\mathrm{5}}=\mathrm{80\%} \\ $$
