
Question Number 195693 by deleteduser4 last updated on 08/Aug/23
![hello [Σ_(n=1) ^(10000) (1/( (√n)))]=? [ ] : is bracket thank you](Q195693.png)
$${hello} \\ $$$$\left[\underset{{n}=\mathrm{1}} {\overset{\mathrm{10000}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{n}}}\right]=? \\ $$$$\left[\:\right]\::\:{is}\:{bracket} \\ $$$${thank}\:{you} \\ $$$$ \\ $$
Commented by York12 last updated on 08/Aug/23
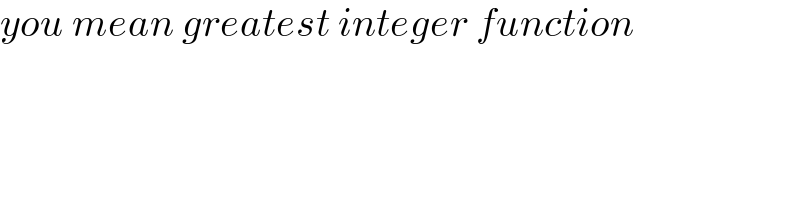
$${you}\:{mean}\:{greatest}\:{integer}\:{function} \\ $$
Answered by MM42 last updated on 08/Aug/23

$$\mathrm{198}\: \\ $$
Commented by deleteduser4 last updated on 09/Aug/23

$${thank}\:{you} \\ $$$${please}\:{give}\:{your}\:{solution} \\ $$
Answered by CrispyXYZ last updated on 09/Aug/23
![(√(n−1))<(√n)<(√(n+1)) ⇒(√n)+(√(n−1))<2(√n)<(√n)+(√(n+1)) ⇒(1/( (√n)+(√(n+1))))<(1/(2(√n)))<(1/( (√(n−1))+(√n))) ⇒2((√(n+1))−(√n))<(1/( (√n)))<2((√n)−(√(n−1))) Therefore, 198=2(100−1)<2((√(10001))−1)<Σ_(n=1) ^(10000) (1/( (√n)))=1 +Σ_(n=2) ^(10000) (1/( (√n)))<1+2(100−1)=199 [Σ_(n=1) ^(10000) (1/( (√n)))]=198](Q195734.png)
$$\sqrt{{n}−\mathrm{1}}<\sqrt{{n}}<\sqrt{{n}+\mathrm{1}} \\ $$$$\Rightarrow\sqrt{{n}}+\sqrt{{n}−\mathrm{1}}<\mathrm{2}\sqrt{{n}}<\sqrt{{n}}+\sqrt{{n}+\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\:\sqrt{{n}}+\sqrt{{n}+\mathrm{1}}}<\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}<\frac{\mathrm{1}}{\:\sqrt{{n}−\mathrm{1}}+\sqrt{{n}}} \\ $$$$\Rightarrow\mathrm{2}\left(\sqrt{{n}+\mathrm{1}}−\sqrt{{n}}\right)<\frac{\mathrm{1}}{\:\sqrt{{n}}}<\mathrm{2}\left(\sqrt{{n}}−\sqrt{{n}−\mathrm{1}}\right) \\ $$$$\mathrm{Therefore}, \\ $$$$\mathrm{198}=\mathrm{2}\left(\mathrm{100}−\mathrm{1}\right)<\mathrm{2}\left(\sqrt{\mathrm{10001}}−\mathrm{1}\right)<\underset{{n}=\mathrm{1}} {\overset{\mathrm{10000}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{n}}}=\mathrm{1} \\ $$$$+\underset{{n}=\mathrm{2}} {\overset{\mathrm{10000}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{n}}}<\mathrm{1}+\mathrm{2}\left(\mathrm{100}−\mathrm{1}\right)=\mathrm{199} \\ $$$$\left[\underset{{n}=\mathrm{1}} {\overset{\mathrm{10000}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{n}}}\right]=\mathrm{198} \\ $$
Commented by MM42 last updated on 09/Aug/23

$$ \\ $$$${good} \\ $$
