
Question Number 66802 by Rio Michael last updated on 19/Aug/19
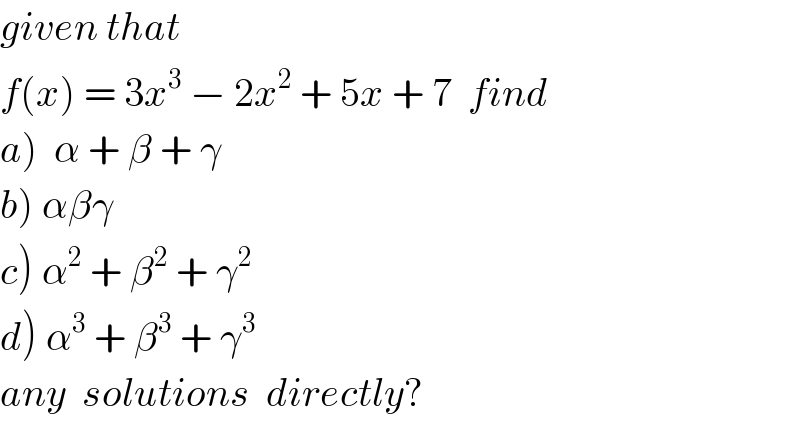
$${given}\:{that}\: \\ $$$${f}\left({x}\right)\:=\:\mathrm{3}{x}^{\mathrm{3}} \:−\:\mathrm{2}{x}^{\mathrm{2}} \:+\:\mathrm{5}{x}\:+\:\mathrm{7}\:\:{find} \\ $$$$\left.{a}\right)\:\:\alpha\:+\:\beta\:+\:\gamma \\ $$$$\left.{b}\right)\:\alpha\beta\gamma\:\: \\ $$$$\left.{c}\right)\:\alpha^{\mathrm{2}} \:+\:\beta^{\mathrm{2}} \:+\:\gamma^{\mathrm{2}} \\ $$$$\left.{d}\right)\:\alpha^{\mathrm{3}} \:+\:\beta^{\mathrm{3}} \:+\:\gamma^{\mathrm{3}} \\ $$$${any}\:\:{solutions}\:\:{directly}? \\ $$
Commented by mathmax by abdo last updated on 19/Aug/19
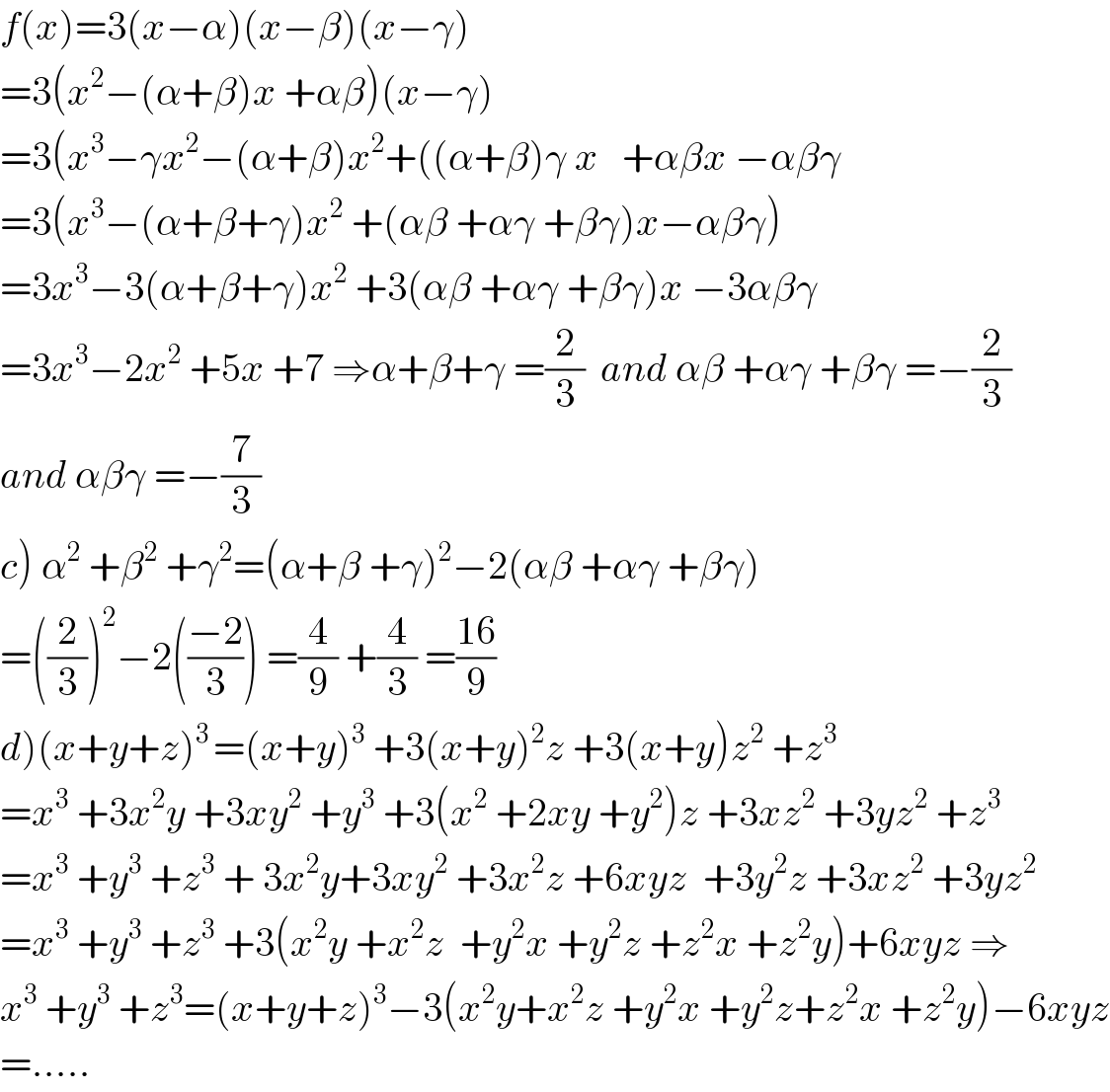
$${f}\left({x}\right)=\mathrm{3}\left({x}−\alpha\right)\left({x}−\beta\right)\left({x}−\gamma\right) \\ $$$$=\mathrm{3}\left({x}^{\mathrm{2}} −\left(\alpha+\beta\right){x}\:+\alpha\beta\right)\left({x}−\gamma\right)\: \\ $$$$=\mathrm{3}\left({x}^{\mathrm{3}} −\gamma{x}^{\mathrm{2}} −\left(\alpha+\beta\right){x}^{\mathrm{2}} +\left(\left(\alpha+\beta\right)\gamma\:{x}\:\:\:+\alpha\beta{x}\:−\alpha\beta\gamma\right.\right. \\ $$$$=\mathrm{3}\left({x}^{\mathrm{3}} −\left(\alpha+\beta+\gamma\right){x}^{\mathrm{2}} \:+\left(\alpha\beta\:+\alpha\gamma\:+\beta\gamma\right){x}−\alpha\beta\gamma\right) \\ $$$$=\mathrm{3}{x}^{\mathrm{3}} −\mathrm{3}\left(\alpha+\beta+\gamma\right){x}^{\mathrm{2}} \:+\mathrm{3}\left(\alpha\beta\:+\alpha\gamma\:+\beta\gamma\right){x}\:−\mathrm{3}\alpha\beta\gamma \\ $$$$=\mathrm{3}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{5}{x}\:+\mathrm{7}\:\Rightarrow\alpha+\beta+\gamma\:=\frac{\mathrm{2}}{\mathrm{3}}\:\:{and}\:\alpha\beta\:+\alpha\gamma\:+\beta\gamma\:=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${and}\:\alpha\beta\gamma\:=−\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\left.{c}\right)\:\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \:+\gamma^{\mathrm{2}} =\left(\alpha+\beta\:+\gamma\right)^{\mathrm{2}} −\mathrm{2}\left(\alpha\beta\:+\alpha\gamma\:+\beta\gamma\right) \\ $$$$=\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{−\mathrm{2}}{\mathrm{3}}\right)\:=\frac{\mathrm{4}}{\mathrm{9}}\:+\frac{\mathrm{4}}{\mathrm{3}}\:=\frac{\mathrm{16}}{\mathrm{9}} \\ $$$$\left.{d}\right)\left({x}+{y}+{z}\right)^{\mathrm{3}\:} =\left({x}+{y}\right)^{\mathrm{3}} \:+\mathrm{3}\left({x}+{y}\right)^{\mathrm{2}} {z}\:+\mathrm{3}\left({x}+{y}\right){z}^{\mathrm{2}} \:+{z}^{\mathrm{3}} \\ $$$$={x}^{\mathrm{3}} \:+\mathrm{3}{x}^{\mathrm{2}} {y}\:+\mathrm{3}{xy}^{\mathrm{2}} \:+{y}^{\mathrm{3}} \:+\mathrm{3}\left({x}^{\mathrm{2}} \:+\mathrm{2}{xy}\:+{y}^{\mathrm{2}} \right){z}\:+\mathrm{3}{xz}^{\mathrm{2}} \:+\mathrm{3}{yz}^{\mathrm{2}} \:+{z}^{\mathrm{3}} \\ $$$$={x}^{\mathrm{3}} \:+{y}^{\mathrm{3}} \:+{z}^{\mathrm{3}} \:+\:\mathrm{3}{x}^{\mathrm{2}} {y}+\mathrm{3}{xy}^{\mathrm{2}} \:+\mathrm{3}{x}^{\mathrm{2}} {z}\:+\mathrm{6}{xyz}\:\:+\mathrm{3}{y}^{\mathrm{2}} {z}\:+\mathrm{3}{xz}^{\mathrm{2}} \:+\mathrm{3}{yz}^{\mathrm{2}} \\ $$$$={x}^{\mathrm{3}} \:+{y}^{\mathrm{3}} \:+{z}^{\mathrm{3}} \:+\mathrm{3}\left({x}^{\mathrm{2}} {y}\:+{x}^{\mathrm{2}} {z}\:\:+{y}^{\mathrm{2}} {x}\:+{y}^{\mathrm{2}} {z}\:+{z}^{\mathrm{2}} {x}\:+{z}^{\mathrm{2}} {y}\right)+\mathrm{6}{xyz}\:\Rightarrow \\ $$$${x}^{\mathrm{3}} \:+{y}^{\mathrm{3}} \:+{z}^{\mathrm{3}} =\left({x}+{y}+{z}\right)^{\mathrm{3}} −\mathrm{3}\left({x}^{\mathrm{2}} {y}+{x}^{\mathrm{2}} {z}\:+{y}^{\mathrm{2}} {x}\:+{y}^{\mathrm{2}} {z}+{z}^{\mathrm{2}} {x}\:+{z}^{\mathrm{2}} {y}\right)−\mathrm{6}{xyz} \\ $$$$=..... \\ $$
Commented by Rio Michael last updated on 20/Aug/19

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 20/Aug/19
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Commented by Kunal12588 last updated on 20/Aug/19
![α^3 +β^3 +γ^3 =(α+β)^3 −3αβ(α+β)+γ^3 =(α+β)^3 +γ^3 −3αβ(α+β) =(α+β+γ)[(α+β)^2 −(α+β)γ+γ^2 ]−3αβ(α+β+γ)+3αβγ =(α+β+γ)(α^2 +β^2 +2αβ−αγ−βγ+γ^2 −3αβ)+3αβγ α^3 +β^3 +γ^3 =(α+β+γ)(α^2 +β^2 +γ^2 −αβ−βγ−γα)+3αβγ α^3 +β^3 +γ^3 =(α+β+γ)^3 −3(α+β+γ)(αβ+βγ+γα))+3αβγ α^3 +β^3 +γ^3 =(1/2)(α+β+γ)((α−β)^2 +(β−γ)^2 +(γ−α)^2 )+3αβγ these formulas can be used to solve α^3 +β^3 +γ^3 =(2/3)(−((26)/9)−(5/3))−7=((−82−189)/(27))=((−271)/(27))](Q66837.png)
$$\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\gamma^{\mathrm{3}} =\left(\alpha+\beta\right)^{\mathrm{3}} −\mathrm{3}\alpha\beta\left(\alpha+\beta\right)+\gamma^{\mathrm{3}} \\ $$$$=\left(\alpha+\beta\right)^{\mathrm{3}} +\gamma^{\mathrm{3}} −\mathrm{3}\alpha\beta\left(\alpha+\beta\right) \\ $$$$=\left(\alpha+\beta+\gamma\right)\left[\left(\alpha+\beta\right)^{\mathrm{2}} −\left(\alpha+\beta\right)\gamma+\gamma^{\mathrm{2}} \right]−\mathrm{3}\alpha\beta\left(\alpha+\beta+\gamma\right)+\mathrm{3}\alpha\beta\gamma \\ $$$$=\left(\alpha+\beta+\gamma\right)\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\mathrm{2}\alpha\beta−\alpha\gamma−\beta\gamma+\gamma^{\mathrm{2}} −\mathrm{3}\alpha\beta\right)+\mathrm{3}\alpha\beta\gamma \\ $$$$\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\gamma^{\mathrm{3}} =\left(\alpha+\beta+\gamma\right)\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} −\alpha\beta−\beta\gamma−\gamma\alpha\right)+\mathrm{3}\alpha\beta\gamma \\ $$$$\left.\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\gamma^{\mathrm{3}} =\left(\alpha+\beta+\gamma\right)^{\mathrm{3}} −\mathrm{3}\left(\alpha+\beta+\gamma\right)\left(\alpha\beta+\beta\gamma+\gamma\alpha\right)\right)+\mathrm{3}\alpha\beta\gamma \\ $$$$\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\gamma^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\alpha+\beta+\gamma\right)\left(\left(\alpha−\beta\right)^{\mathrm{2}} +\left(\beta−\gamma\right)^{\mathrm{2}} +\left(\gamma−\alpha\right)^{\mathrm{2}} \right)+\mathrm{3}\alpha\beta\gamma \\ $$$${these}\:{formulas}\:{can}\:{be}\:{used}\:{to}\:{solve} \\ $$$$\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\gamma^{\mathrm{3}} =\frac{\mathrm{2}}{\mathrm{3}}\left(−\frac{\mathrm{26}}{\mathrm{9}}−\frac{\mathrm{5}}{\mathrm{3}}\right)−\mathrm{7}=\frac{−\mathrm{82}−\mathrm{189}}{\mathrm{27}}=\frac{−\mathrm{271}}{\mathrm{27}} \\ $$
Commented by mathmax by abdo last updated on 20/Aug/19
$${thank}\:{you}\:{kunal}\:{for}\:{completing}... \\ $$
Commented by Kunal12588 last updated on 20/Aug/19
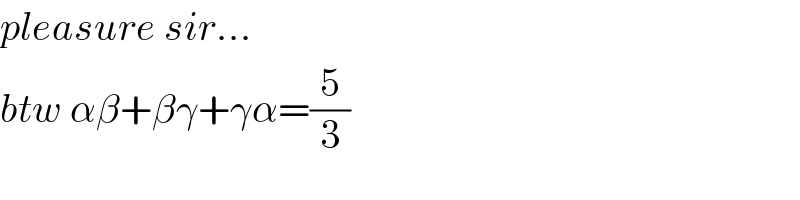
$${pleasure}\:{sir}... \\ $$$${btw}\:\alpha\beta+\beta\gamma+\gamma\alpha=\frac{\mathrm{5}}{\mathrm{3}} \\ $$
