Question and Answers Forum

All Questions      Topic List

Set Theory Questions

Previous in All Question      Next in All Question      

Previous in Set Theory      Next in Set Theory      

Question Number 216355 by jikansamu last updated on 05/Feb/25

given that ϕ,β are the roots of the equation 3x2−x−5=0 from the equation whose roots are 2ϕ−1/β,2β−1/ϕ

$${given}\:{that}\:\varphi,\beta\:{are}\:{the}\:{roots}\:{of}\:{the}\:{equation}\:\mathrm{3}{x}\mathrm{2}−{x}−\mathrm{5}=\mathrm{0}\:{from}\:{the}\:{equation}\:{whose}\:{roots}\:{are}\:\mathrm{2}\varphi−\mathrm{1}/\beta,\mathrm{2}\beta−\mathrm{1}/\varphi \\ $$

Commented by AntonCWX last updated on 05/Feb/25

Please make sure to have your question typed neatly and in quality.

$${Please}\:{make}\:{sure}\:{to}\:{have}\:{your}\:{question}\:{typed}\:{neatly}\:{and}\:{in}\:{quality}. \\ $$

Answered by AntonCWX last updated on 05/Feb/25

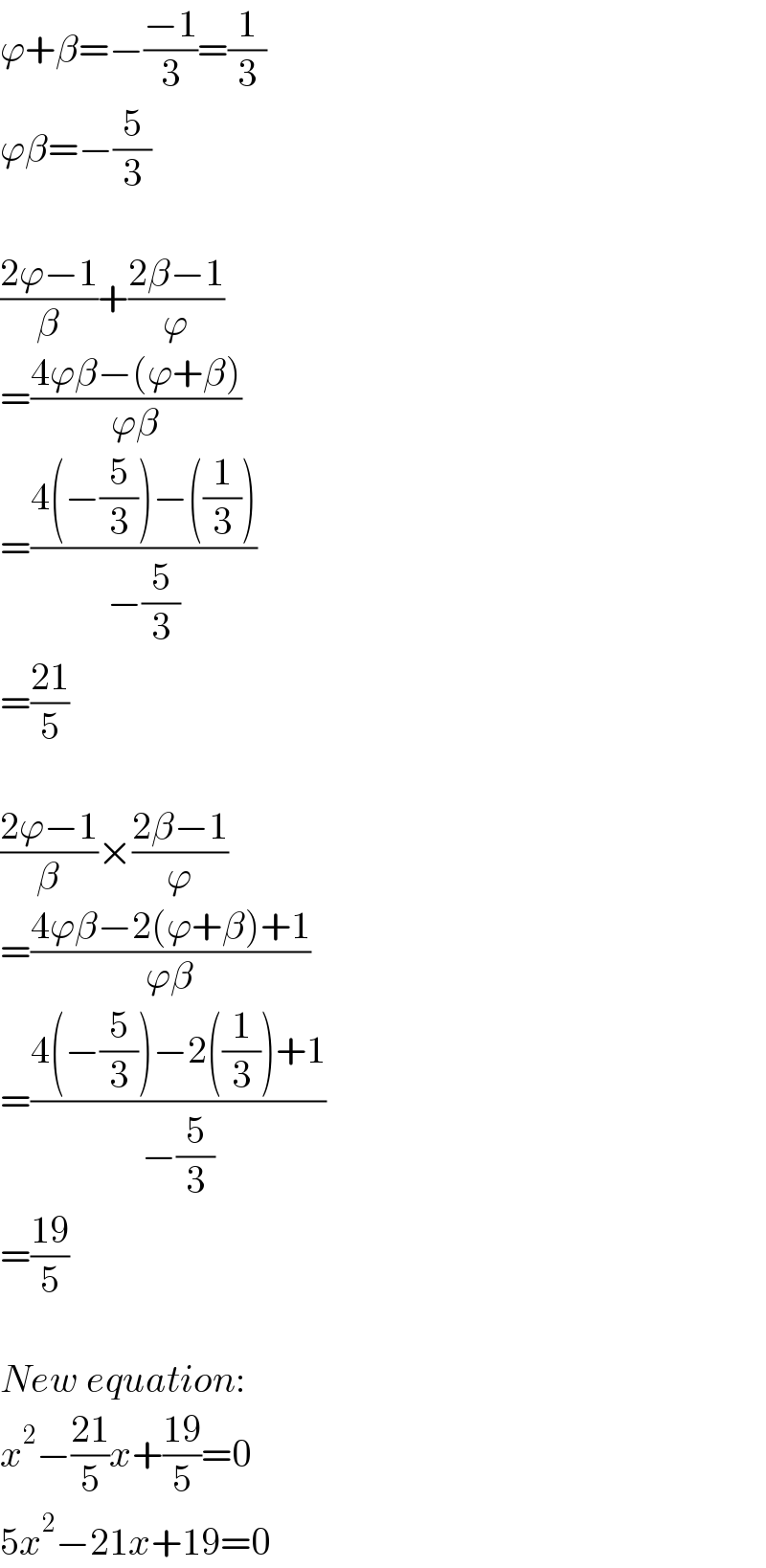
ϕ+β=−((−1)/3)=(1/3) ϕβ=−(5/3) ((2ϕ−1)/β)+((2β−1)/ϕ) =((4ϕβ−(ϕ+β))/(ϕβ)) =((4(−(5/3))−((1/3)))/(−(5/3))) =((21)/5) ((2ϕ−1)/β)×((2β−1)/ϕ) =((4ϕβ−2(ϕ+β)+1)/(ϕβ)) =((4(−(5/3))−2((1/3))+1)/(−(5/3))) =((19)/5) New equation: x^2 −((21)/5)x+((19)/5)=0 5x^2 −21x+19=0

$$\varphi+\beta=−\frac{−\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\varphi\beta=−\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$ \\ $$$$\frac{\mathrm{2}\varphi−\mathrm{1}}{\beta}+\frac{\mathrm{2}\beta−\mathrm{1}}{\varphi} \\ $$$$=\frac{\mathrm{4}\varphi\beta−\left(\varphi+\beta\right)}{\varphi\beta} \\ $$$$=\frac{\mathrm{4}\left(−\frac{\mathrm{5}}{\mathrm{3}}\right)−\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{−\frac{\mathrm{5}}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{21}}{\mathrm{5}} \\ $$$$ \\ $$$$\frac{\mathrm{2}\varphi−\mathrm{1}}{\beta}×\frac{\mathrm{2}\beta−\mathrm{1}}{\varphi} \\ $$$$=\frac{\mathrm{4}\varphi\beta−\mathrm{2}\left(\varphi+\beta\right)+\mathrm{1}}{\varphi\beta} \\ $$$$=\frac{\mathrm{4}\left(−\frac{\mathrm{5}}{\mathrm{3}}\right)−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{1}}{−\frac{\mathrm{5}}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{19}}{\mathrm{5}} \\ $$$$ \\ $$$${New}\:{equation}: \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{21}}{\mathrm{5}}{x}+\frac{\mathrm{19}}{\mathrm{5}}=\mathrm{0} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{19}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com