
Question Number 72718 by Rio Michael last updated on 01/Nov/19
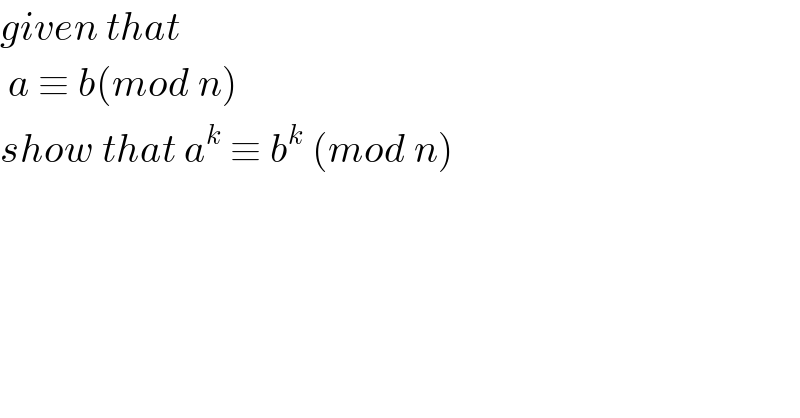
$${given}\:{that}\: \\ $$$$\:{a}\:\equiv\:{b}\left({mod}\:{n}\right)\: \\ $$$${show}\:{that}\:{a}^{{k}} \:\equiv\:{b}^{{k}} \:\left({mod}\:{n}\right) \\ $$
Commented by prof Abdo imad last updated on 01/Nov/19
![⇒a−b=qn ⇒a=qn+b ⇒a^k =(qn+b)^k =Σ_(p=0) ^k C_k ^p (qn)^p b^(k−p) =b^k +Σ_(p=1) ^k C_k ^p (qn)^p b^(k−p) a^k −b^k =n Σ_(p=1) ^k C_p ^k q^p n^(p−1) b^(k−p) ≡0[n] ⇒ a^k ≡b^k [n].](Q72719.png)
$$\Rightarrow{a}−{b}={qn}\:\Rightarrow{a}={qn}+{b}\:\Rightarrow{a}^{{k}} =\left({qn}+{b}\right)^{{k}} \\ $$$$=\sum_{{p}=\mathrm{0}} ^{{k}} \:{C}_{{k}} ^{{p}} \:\left({qn}\right)^{{p}} {b}^{{k}−{p}} ={b}^{{k}} \:+\sum_{{p}=\mathrm{1}} ^{{k}} \:{C}_{{k}} ^{{p}} \left({qn}\right)^{{p}} \:{b}^{{k}−{p}} \\ $$$${a}^{{k}} −{b}^{{k}} \:={n}\:\sum_{{p}=\mathrm{1}} ^{{k}} \:{C}_{{p}} ^{{k}} \:{q}^{{p}} {n}^{{p}−\mathrm{1}} {b}^{{k}−{p}} \:\:\:\equiv\mathrm{0}\left[{n}\right]\:\Rightarrow \\ $$$${a}^{{k}} \equiv{b}^{{k}} \left[{n}\right]. \\ $$$$ \\ $$
Commented by Rio Michael last updated on 01/Nov/19

$${thank}\:{you} \\ $$
Commented by mathmax by abdo last updated on 01/Nov/19
$${you}\:{are}\:{welcome}. \\ $$
