
Question Number 68616 by Rio Michael last updated on 14/Sep/19
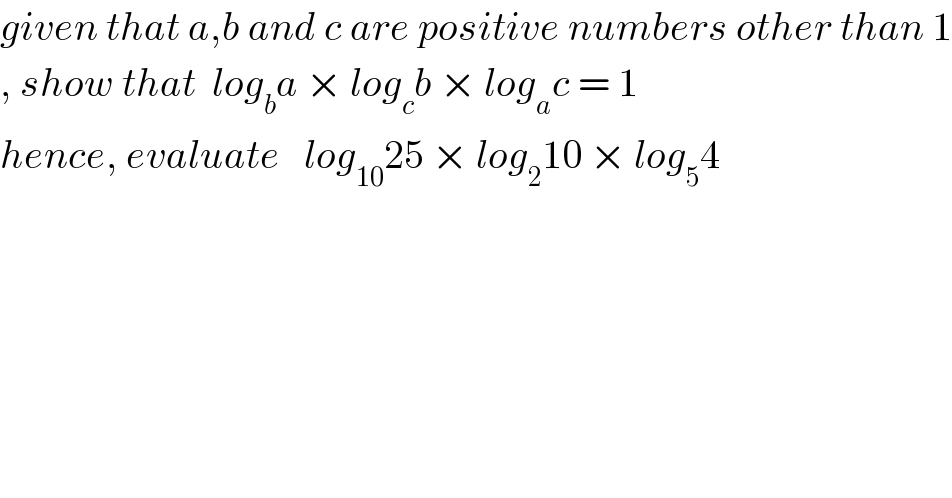
$${given}\:{that}\:{a},{b}\:{and}\:{c}\:{are}\:{positive}\:{numbers}\:{other}\:{than}\:\mathrm{1} \\ $$$$,\:{show}\:{that}\:\:{log}_{{b}} {a}\:×\:{log}_{{c}} {b}\:×\:{log}_{{a}} {c}\:=\:\mathrm{1} \\ $$$${hence},\:{evaluate}\:\:\:{log}_{\mathrm{10}} \mathrm{25}\:×\:{log}_{\mathrm{2}} \mathrm{10}\:×\:{log}_{\mathrm{5}} \mathrm{4} \\ $$
Answered by $@ty@m123 last updated on 14/Sep/19
![Let log_b a=x, log_c b=y, log_a c=z ⇒b^x =a, c^y =b, a^z =c Now, a^z =c [((Note: you can proceed)),((with b^x =a or c^y =b also.)) ] ⇒(b^x )^z =c ⇒(c^y )^(xz) =c ⇒c^(xyz) =c ⇒xyz=1 ⇒log_b a × log_c b × log_a c = 1](Q68621.png)
$${Let}\:\mathrm{log}_{{b}} \:{a}={x},\:\:{log}_{{c}} {b}={y},\:{log}_{{a}} {c}={z} \\ $$$$\Rightarrow{b}^{{x}} ={a},\:{c}^{{y}} ={b},\:{a}^{{z}} ={c} \\ $$$${Now}, \\ $$$${a}^{{z}} ={c}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{bmatrix}{{Note}:\:{you}\:{can}\:{proceed}}\\{{with}\:{b}^{{x}} ={a}\:{or}\:{c}^{{y}} ={b}\:{also}.}\end{bmatrix} \\ $$$$\Rightarrow\left({b}^{{x}} \right)^{{z}} ={c}\:\:\:\: \\ $$$$\Rightarrow\left({c}^{{y}} \right)^{{xz}} ={c} \\ $$$$\Rightarrow{c}^{{xyz}} ={c} \\ $$$$\Rightarrow{xyz}=\mathrm{1} \\ $$$$\Rightarrow{log}_{{b}} {a}\:×\:{log}_{{c}} {b}\:×\:{log}_{{a}} {c}\:=\:\mathrm{1} \\ $$
Answered by $@ty@m123 last updated on 14/Sep/19
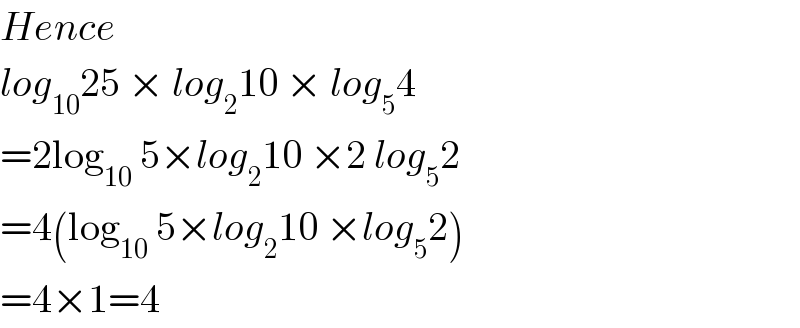
$${Hence} \\ $$$${log}_{\mathrm{10}} \mathrm{25}\:×\:{log}_{\mathrm{2}} \mathrm{10}\:×\:{log}_{\mathrm{5}} \mathrm{4} \\ $$$$=\mathrm{2log}_{\mathrm{10}} \:\mathrm{5}×{log}_{\mathrm{2}} \mathrm{10}\:×\mathrm{2}\:{log}_{\mathrm{5}} \mathrm{2} \\ $$$$=\mathrm{4}\left(\mathrm{log}_{\mathrm{10}} \:\mathrm{5}×{log}_{\mathrm{2}} \mathrm{10}\:×{log}_{\mathrm{5}} \mathrm{2}\right) \\ $$$$=\mathrm{4}×\mathrm{1}=\mathrm{4} \\ $$
Commented by Rio Michael last updated on 14/Sep/19

$${thanks}\:{so}\:{much} \\ $$
