
Question Number 77687 by jagoll last updated on 09/Jan/20
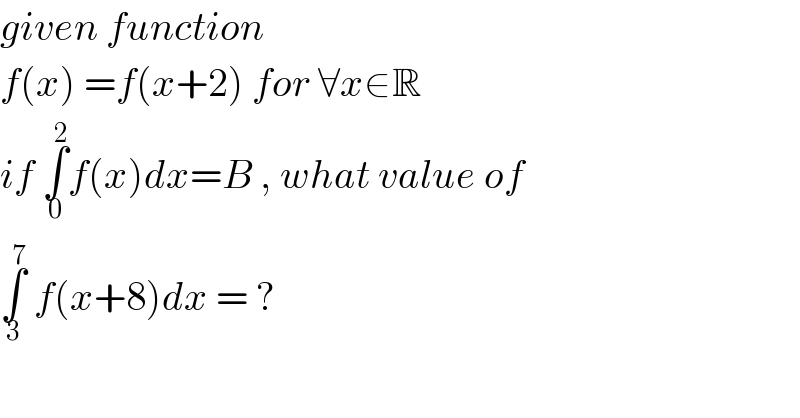
$${given}\:{function} \\ $$$${f}\left({x}\right)\:={f}\left({x}+\mathrm{2}\right)\:{for}\:\forall{x}\in\mathbb{R} \\ $$$${if}\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}={B}\:,\:{what}\:{value}\:{of} \\ $$$$\underset{\mathrm{3}} {\overset{\mathrm{7}} {\int}}\:{f}\left({x}+\mathrm{8}\right){dx}\:=\:? \\ $$
Commented by mr W last updated on 09/Jan/20
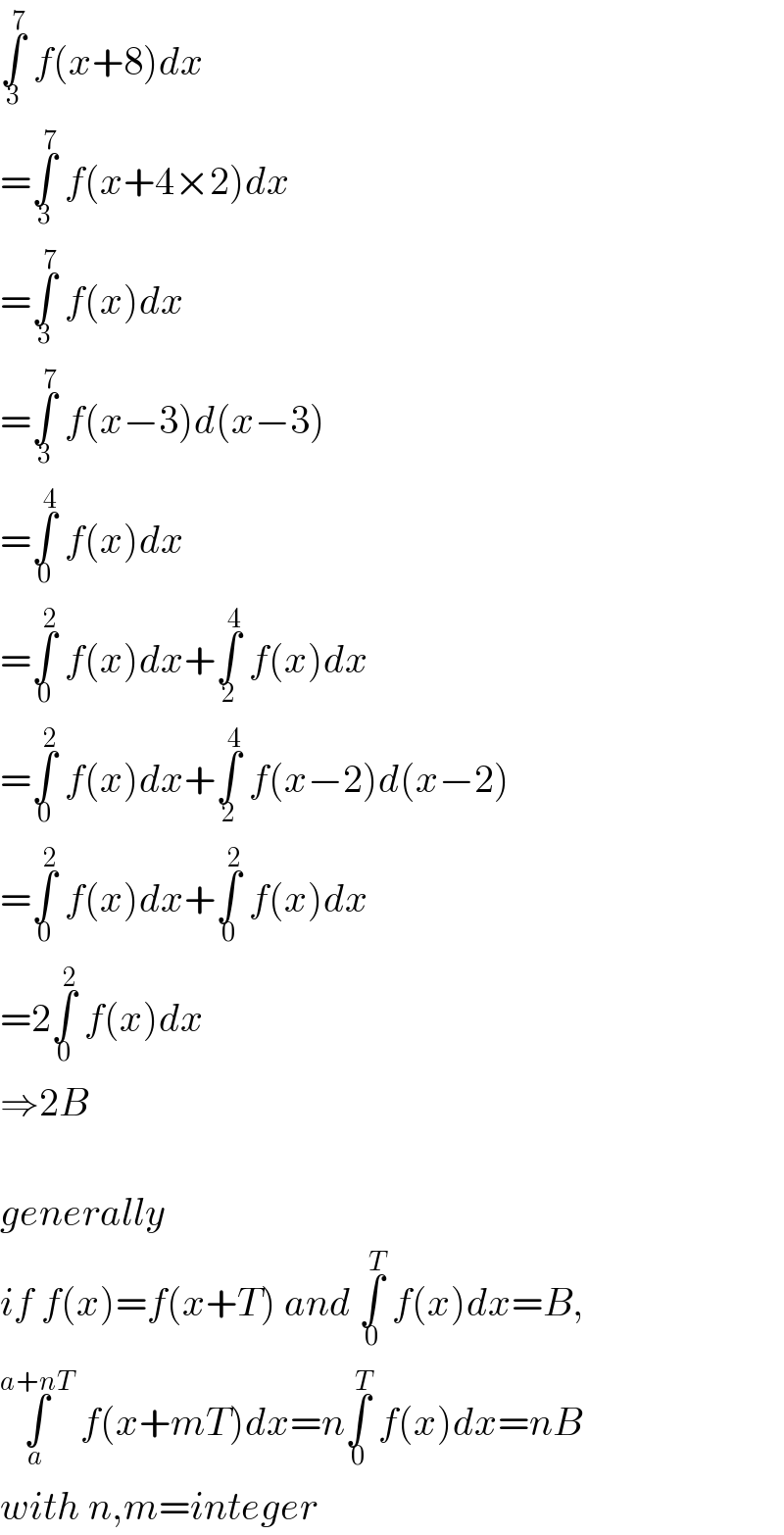
$$\underset{\mathrm{3}} {\overset{\mathrm{7}} {\int}}\:{f}\left({x}+\mathrm{8}\right){dx} \\ $$$$=\underset{\mathrm{3}} {\overset{\mathrm{7}} {\int}}\:{f}\left({x}+\mathrm{4}×\mathrm{2}\right){dx} \\ $$$$=\underset{\mathrm{3}} {\overset{\mathrm{7}} {\int}}\:{f}\left({x}\right){dx} \\ $$$$=\underset{\mathrm{3}} {\overset{\mathrm{7}} {\int}}\:{f}\left({x}−\mathrm{3}\right){d}\left({x}−\mathrm{3}\right) \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}\right){dx} \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{f}\left({x}\right){dx}+\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}\right){dx} \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{f}\left({x}\right){dx}+\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}−\mathrm{2}\right){d}\left({x}−\mathrm{2}\right) \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{f}\left({x}\right){dx}+\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{f}\left({x}\right){dx} \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:{f}\left({x}\right){dx} \\ $$$$\Rightarrow\mathrm{2}{B} \\ $$$$ \\ $$$${generally} \\ $$$${if}\:{f}\left({x}\right)={f}\left({x}+{T}\right)\:{and}\:\underset{\mathrm{0}} {\overset{{T}} {\int}}\:{f}\left({x}\right){dx}={B}, \\ $$$$\underset{{a}} {\overset{{a}+{nT}} {\int}}\:{f}\left({x}+{mT}\right){dx}={n}\underset{\mathrm{0}} {\overset{{T}} {\int}}\:{f}\left({x}\right){dx}={nB} \\ $$$${with}\:{n},{m}={integer} \\ $$
Commented by jagoll last updated on 09/Jan/20

$${thanks}\:{you}\:{sir} \\ $$
Commented by jagoll last updated on 09/Jan/20
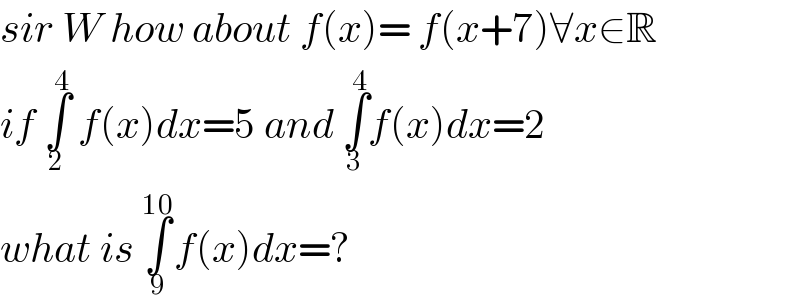
$${sir}\:{W}\:{how}\:{about}\:{f}\left({x}\right)=\:{f}\left({x}+\mathrm{7}\right)\forall{x}\in\mathbb{R} \\ $$$${if}\:\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}\right){dx}=\mathrm{5}\:{and}\:\underset{\mathrm{3}} {\overset{\mathrm{4}} {\int}}{f}\left({x}\right){dx}=\mathrm{2}\: \\ $$$${what}\:{is}\:\underset{\mathrm{9}} {\overset{\mathrm{10}} {\int}}{f}\left({x}\right){dx}=? \\ $$
Commented by mr W last updated on 09/Jan/20
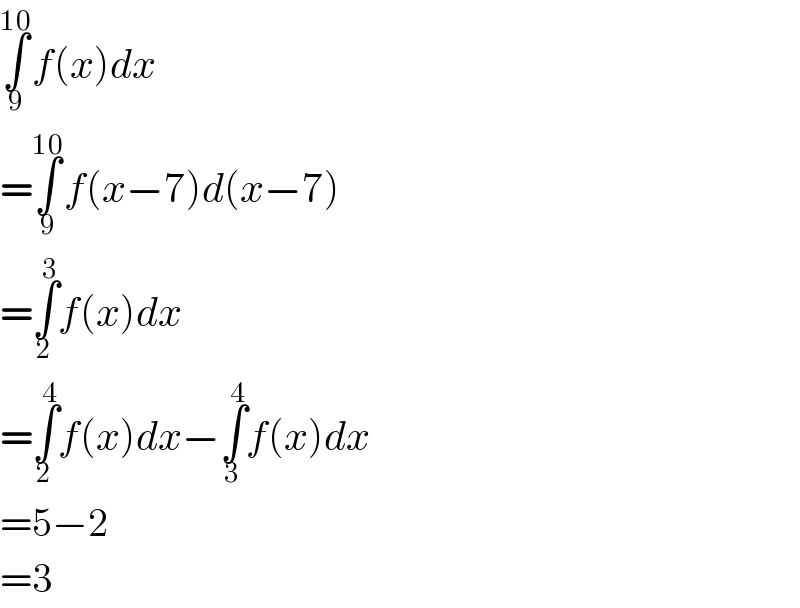
$$\underset{\mathrm{9}} {\overset{\mathrm{10}} {\int}}{f}\left({x}\right){dx} \\ $$$$=\underset{\mathrm{9}} {\overset{\mathrm{10}} {\int}}{f}\left({x}−\mathrm{7}\right){d}\left({x}−\mathrm{7}\right) \\ $$$$=\underset{\mathrm{2}} {\overset{\mathrm{3}} {\int}}{f}\left({x}\right){dx} \\ $$$$=\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}{f}\left({x}\right){dx}−\underset{\mathrm{3}} {\overset{\mathrm{4}} {\int}}{f}\left({x}\right){dx} \\ $$$$=\mathrm{5}−\mathrm{2} \\ $$$$=\mathrm{3} \\ $$
Commented by jagoll last updated on 09/Jan/20

$${thanks}\:{you}\:{sir} \\ $$
Commented by jagoll last updated on 09/Jan/20
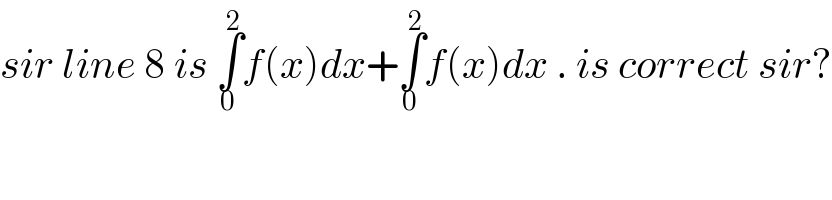
$${sir}\:{line}\:\mathrm{8}\:{is}\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}+\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}\:.\:{is}\:{correct}\:{sir}? \\ $$
Commented by jagoll last updated on 09/Jan/20
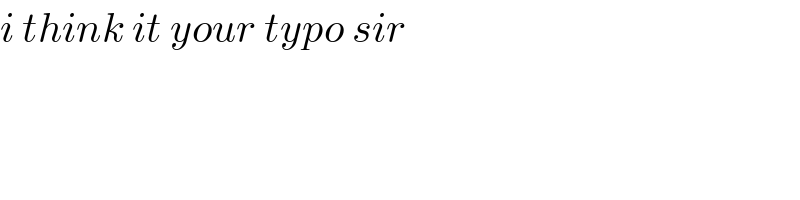
$${i}\:{think}\:{it}\:{your}\:{typo}\:{sir} \\ $$
Commented by mr W last updated on 09/Jan/20

$${yes},\:{now}\:{fixed}! \\ $$
