
Question Number 78829 by jagoll last updated on 21/Jan/20
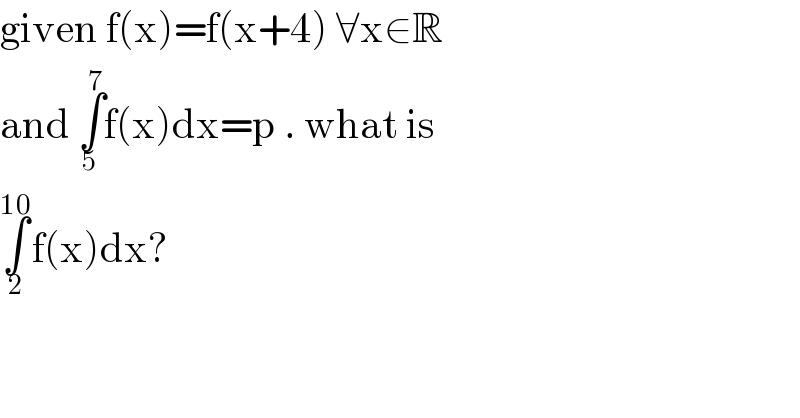
$$\mathrm{given}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}+\mathrm{4}\right)\:\forall\mathrm{x}\in\mathbb{R} \\ $$$$\mathrm{and}\:\underset{\mathrm{5}} {\overset{\mathrm{7}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{p}\:.\:\mathrm{what}\:\mathrm{is}\: \\ $$$$\underset{\mathrm{2}} {\overset{\mathrm{10}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}? \\ $$$$ \\ $$
Commented by jagoll last updated on 21/Jan/20
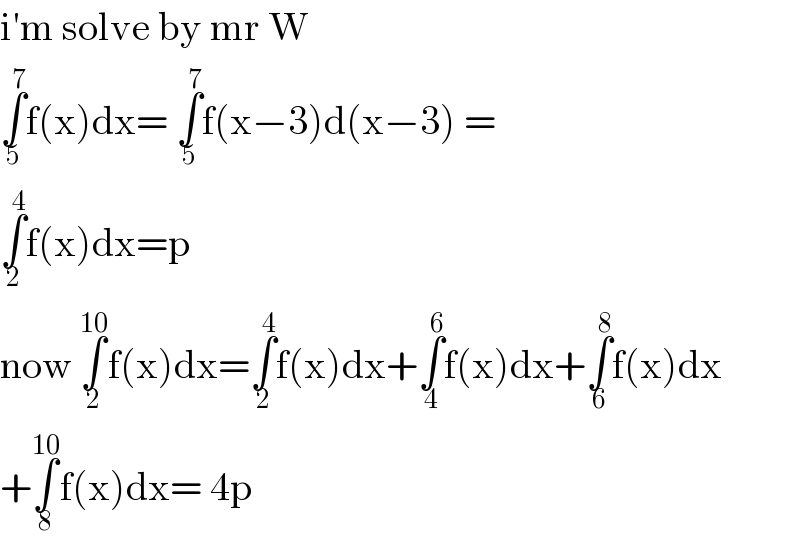
$$\mathrm{i}'\mathrm{m}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{mr}\:\mathrm{W}\: \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{7}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\:\underset{\mathrm{5}} {\overset{\mathrm{7}} {\int}}\mathrm{f}\left(\mathrm{x}−\mathrm{3}\right)\mathrm{d}\left(\mathrm{x}−\mathrm{3}\right)\:= \\ $$$$\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{p} \\ $$$$\mathrm{now}\:\underset{\mathrm{2}} {\overset{\mathrm{10}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}+\underset{\mathrm{4}} {\overset{\mathrm{6}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}+\underset{\mathrm{6}} {\overset{\mathrm{8}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$+\underset{\mathrm{8}} {\overset{\mathrm{10}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\:\mathrm{4p} \\ $$
Commented by jagoll last updated on 21/Jan/20

$$\mathrm{mr}\:\mathrm{W} \\ $$$$\mathrm{my}\:\mathrm{answer}\:\mathrm{correct}? \\ $$
Commented by mr W last updated on 21/Jan/20

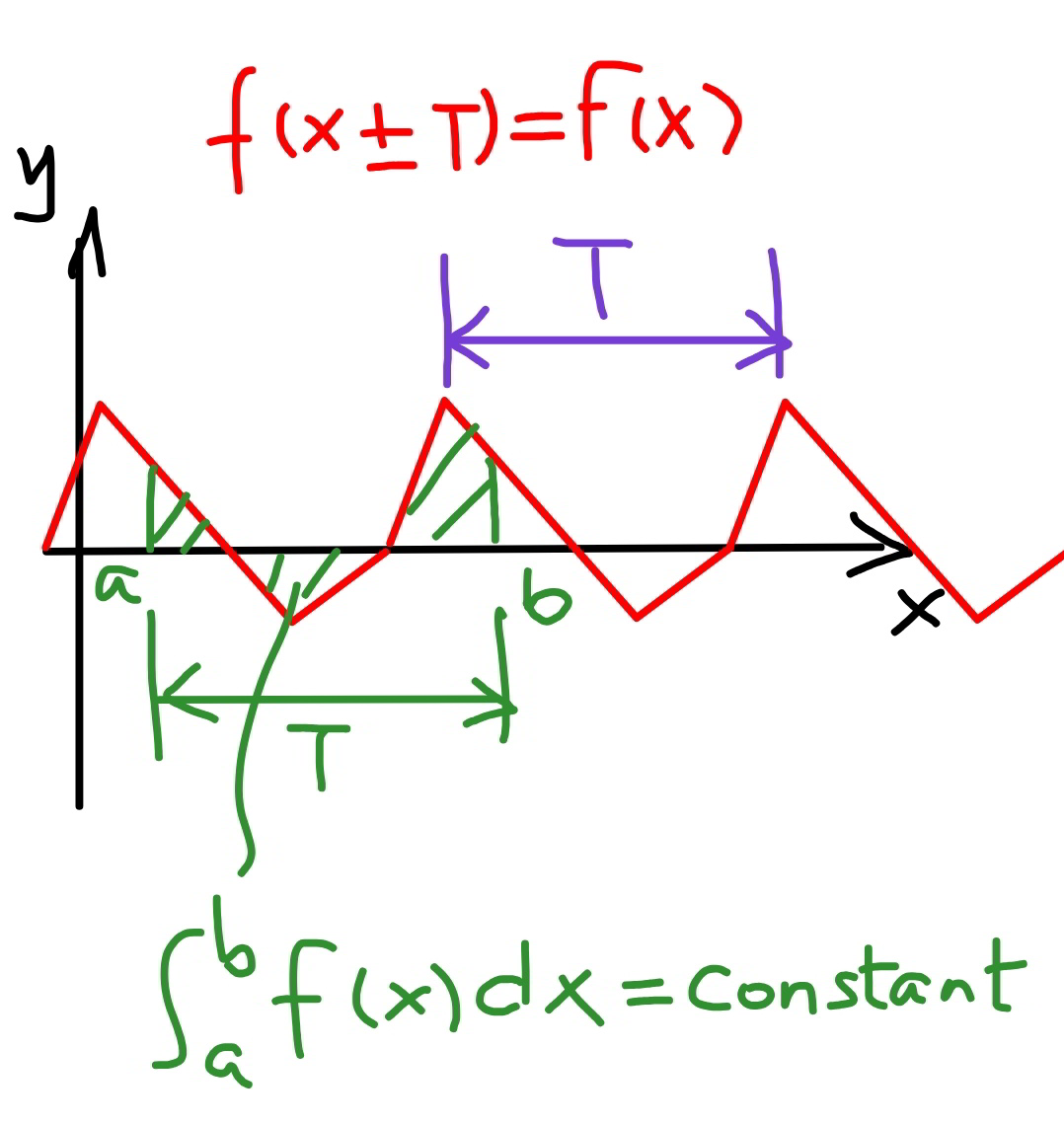
$${the}\:{basic}\:{is}: \\ $$$${for}\:{a}\:{periodic}\:{function}\:{f}\left({x}\right)\:{with} \\ $$$${period}\:{T},\:{i}.{e}.\:{f}\left({x}\right)={f}\left({x}+{T}\right),\:{the} \\ $$$${integral}\:{over}\:{a}\:{length}\:{of}\:{T}\:{is}\:{always} \\ $$$${the}\:{same},\:{indepedently}\:{from}\:{the} \\ $$$${start}\:{point}\:{of}\:{the}\:{integral}. \\ $$$${see}\:{diagram}. \\ $$$${e}.{g}.\:{if}\:{the}\:{period}\:{is}\:\mathrm{4},\:{i}.{e}.\:{f}\left({x}\right)={f}\left({x}+\mathrm{4}\right), \\ $$$${we}\:{have} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{5}} {f}\left({x}\right){dx}=\int_{\mathrm{3}} ^{\mathrm{7}} {f}\left({x}\right){dx}=\int_{{a}} ^{{a}+\mathrm{4}} {f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}\right){dx} \\ $$$${we}\:{have}\:{also} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{13}} {f}\left({x}\right){dx}=\int_{\mathrm{3}} ^{\mathrm{15}} {f}\left({x}\right){dx}=\int_{{a}} ^{{a}+\mathrm{12}} {f}\left({x}\right)=\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}\right){dx} \\ $$$${etc}. \\ $$$${keep}\:{in}\:{mind}:\:{we}\:{should}\:{alway}\:{take} \\ $$$${one}\:{or}\:{more}\:``{whole}''\:{periods}!\: \\ $$$${e}.{g}.\:\int_{\mathrm{1}} ^{\mathrm{4}} {f}\left({x}\right){dx}\neq\int_{\mathrm{3}} ^{\mathrm{6}} {f}\left({x}\right){dx} \\ $$
Commented by mr W last updated on 21/Jan/20
Commented by mr W last updated on 21/Jan/20

$${therefore}\:{your}\:{answer}\:{is}\:{not}\:{correct}. \\ $$$${and}\:{for}\:{a}\:{function}\:{with}\:{period}\:\mathrm{4},\:{if} \\ $$$${only}\:\int_{\mathrm{5}} ^{\mathrm{7}} {f}\left({x}\right){dx}\:{is}\:{given},\:{it}'{s}\:{not}\:{possible} \\ $$$${to}\:{find}\:{out}\:\int_{\mathrm{2}} ^{\mathrm{10}} {f}\left({x}\right){dx}. \\ $$
Commented by mr W last updated on 21/Jan/20
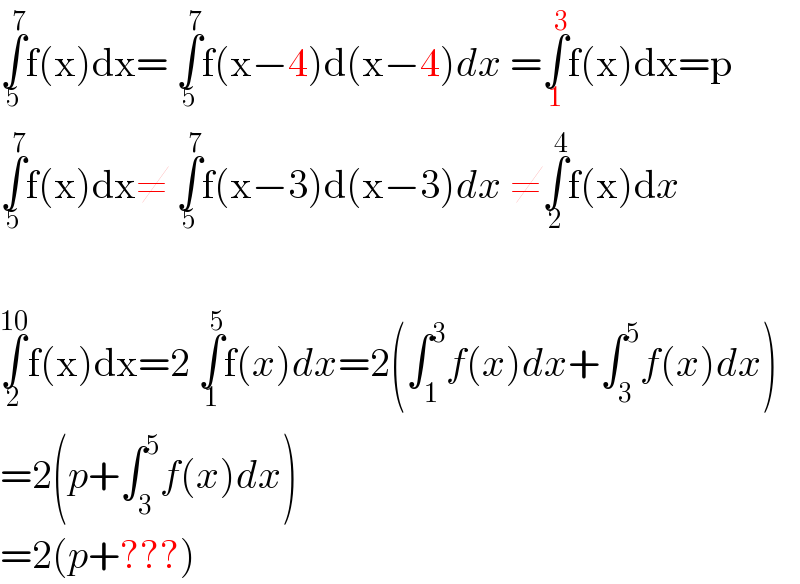
$$\underset{\mathrm{5}} {\overset{\mathrm{7}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\:\underset{\mathrm{5}} {\overset{\mathrm{7}} {\int}}\mathrm{f}\left(\mathrm{x}−\mathrm{4}\right)\mathrm{d}\left(\mathrm{x}−\mathrm{4}\right){dx}\:=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{p} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{7}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\neq\:\underset{\mathrm{5}} {\overset{\mathrm{7}} {\int}}\mathrm{f}\left(\mathrm{x}−\mathrm{3}\right)\mathrm{d}\left(\mathrm{x}−\mathrm{3}\right){dx}\:\neq\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{d}{x} \\ $$$$ \\ $$$$\underset{\mathrm{2}} {\overset{\mathrm{10}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{2}\:\underset{\mathrm{1}} {\overset{\mathrm{5}} {\int}}\mathrm{f}\left({x}\right){dx}=\mathrm{2}\left(\int_{\mathrm{1}} ^{\mathrm{3}} {f}\left({x}\right){dx}+\int_{\mathrm{3}} ^{\mathrm{5}} {f}\left({x}\right){dx}\right) \\ $$$$=\mathrm{2}\left({p}+\int_{\mathrm{3}} ^{\mathrm{5}} {f}\left({x}\right){dx}\right) \\ $$$$=\mathrm{2}\left({p}+???\right) \\ $$
Commented by jagoll last updated on 21/Jan/20
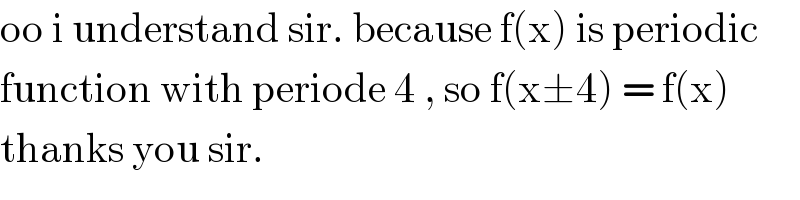
$$\mathrm{oo}\:\mathrm{i}\:\mathrm{understand}\:\mathrm{sir}.\:\mathrm{because}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{periodic} \\ $$$$\mathrm{function}\:\mathrm{with}\:\mathrm{periode}\:\mathrm{4}\:,\:\mathrm{so}\:\mathrm{f}\left(\mathrm{x}\pm\mathrm{4}\right)\:=\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{thanks}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$
Commented by mr W last updated on 21/Jan/20

$${that}'{s}\:{right}! \\ $$
