
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 81219 by jagoll last updated on 10/Feb/20
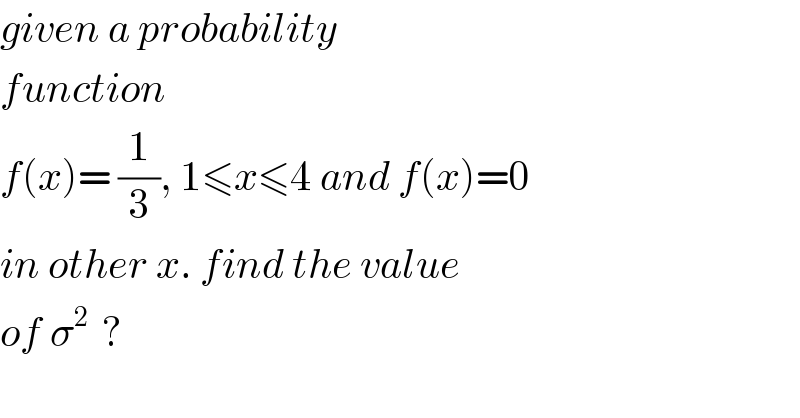
$${given}\:{a}\:{probability}\: \\ $$$${function}\: \\ $$$${f}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{3}},\:\mathrm{1}\leqslant{x}\leqslant\mathrm{4}\:{and}\:{f}\left({x}\right)=\mathrm{0} \\ $$$${in}\:{other}\:{x}.\:{find}\:{the}\:{value}\: \\ $$$${of}\:\sigma^{\mathrm{2}\:} \:? \\ $$
Commented by jagoll last updated on 10/Feb/20
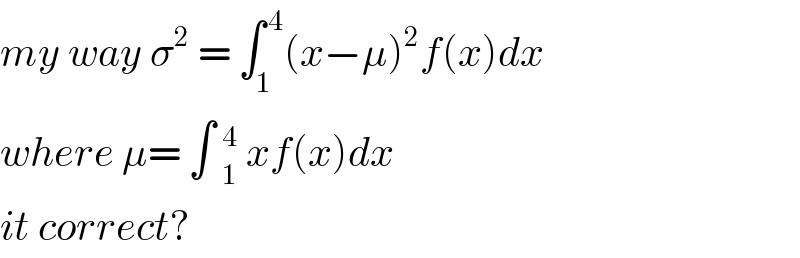
$${my}\:{way}\:\sigma^{\mathrm{2}} \:=\:\int_{\mathrm{1}} ^{\:\mathrm{4}} \left({x}−\mu\right)^{\mathrm{2}} {f}\left({x}\right){dx} \\ $$$${where}\:\mu=\:\int\:_{\mathrm{1}} ^{\mathrm{4}} \:{xf}\left({x}\right){dx} \\ $$$${it}\:{correct}? \\ $$
Commented by Joel578 last updated on 10/Feb/20

$${yes} \\ $$
Commented by Joel578 last updated on 10/Feb/20
![another formula σ_X ^2 = ∫_(−∞) ^∞ (x − μ)^2 f(x) dx = ∫_(−∞) ^∞ (x^2 − 2xμ + μ^2 )f(x) dx = ∫_(−∞) ^∞ x^2 f(x) dx − 2μ ∫_(−∞) ^∞ x f(x) dx + μ^2 ∫_(−∞) ^∞ f(x) dx = ∫_(−∞) ^∞ x^2 f(x) dx − 2μ . μ + μ^2 . 1 = ∫_(−∞) ^∞ x^2 f(x) dx − μ^2 = E[X^2 ] − μ^2](Q81241.png)
$${another}\:{formula} \\ $$$$\sigma_{{X}} ^{\mathrm{2}} \:=\:\underset{−\infty} {\overset{\infty} {\int}}\:\left({x}\:−\:\mu\right)^{\mathrm{2}} \:{f}\left({x}\right)\:{dx} \\ $$$$\:\:\:\:\:\:\:=\:\underset{−\infty} {\overset{\infty} {\int}}\:\left({x}^{\mathrm{2}} \:−\:\mathrm{2}{x}\mu\:+\:\mu^{\mathrm{2}} \right){f}\left({x}\right)\:{dx} \\ $$$$\:\:\:\:\:\:\:=\:\underset{−\infty} {\overset{\infty} {\int}}{x}^{\mathrm{2}} \:{f}\left({x}\right)\:{dx}\:−\:\mathrm{2}\mu\:\underset{−\infty} {\overset{\infty} {\int}}{x}\:{f}\left({x}\right)\:{dx}\:+\:\mu^{\mathrm{2}} \:\underset{−\infty} {\overset{\infty} {\int}}{f}\left({x}\right)\:{dx} \\ $$$$\:\:\:\:\:\:\:=\:\underset{−\infty} {\overset{\infty} {\int}}{x}^{\mathrm{2}} \:{f}\left({x}\right)\:{dx}\:−\:\mathrm{2}\mu\:.\:\mu\:+\:\mu^{\mathrm{2}} \:.\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:=\:\underset{−\infty} {\overset{\infty} {\int}}\:{x}^{\mathrm{2}} \:{f}\left({x}\right)\:{dx}\:−\:\mu^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\:{E}\left[{X}^{\mathrm{2}} \right]\:−\:\mu^{\mathrm{2}} \\ $$
Commented by jagoll last updated on 10/Feb/20

$${o}\:{yes}\:{thank}\:{you} \\ $$
Answered by Joel578 last updated on 10/Feb/20
![f_X (x) = { (((1/3) , 1 ≤ x ≤ 4)),(( 0 , elsewhere)) :} E[X] = μ = ∫_(−∞) ^∞ x f(x) dx = ∫_1 ^4 x((1/3)) dx = (5/2) E[X^2 ] = ∫_(−∞) ^∞ x^2 f(x) dx = ∫_1 ^4 x^2 ((1/3)) dx = 7 σ_X ^2 = E[X^2 ] − μ^2 = 7 − ((25)/4) = (3/4)](Q81239.png)
$${f}_{{X}} \left({x}\right)\:=\:\begin{cases}{\frac{\mathrm{1}}{\mathrm{3}}\:\:\:,\:\mathrm{1}\:\leqslant\:{x}\:\leqslant\:\mathrm{4}}\\{\:\mathrm{0}\:\:\:\:\:,\:\mathrm{elsewhere}}\end{cases} \\ $$$$ \\ $$$${E}\left[{X}\right]\:=\:\mu\:=\:\:\underset{−\infty} {\overset{\infty} {\int}}\:{x}\:{f}\left({x}\right)\:{dx}\:=\:\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\:{x}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:{dx}\:=\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${E}\left[{X}^{\mathrm{2}} \right]\:=\:\underset{−\infty} {\overset{\infty} {\int}}{x}^{\mathrm{2}} \:{f}\left({x}\right)\:{dx}\:=\:\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\:{x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:{dx}\:=\:\mathrm{7} \\ $$$$ \\ $$$$\sigma_{{X}} ^{\mathrm{2}} \:=\:{E}\left[{X}^{\mathrm{2}} \right]\:−\:\mu^{\mathrm{2}} \:=\:\mathrm{7}\:−\:\frac{\mathrm{25}}{\mathrm{4}}\:=\:\frac{\mathrm{3}}{\mathrm{4}}\: \\ $$
