
Question Number 33988 by abdo imad last updated on 28/Apr/18
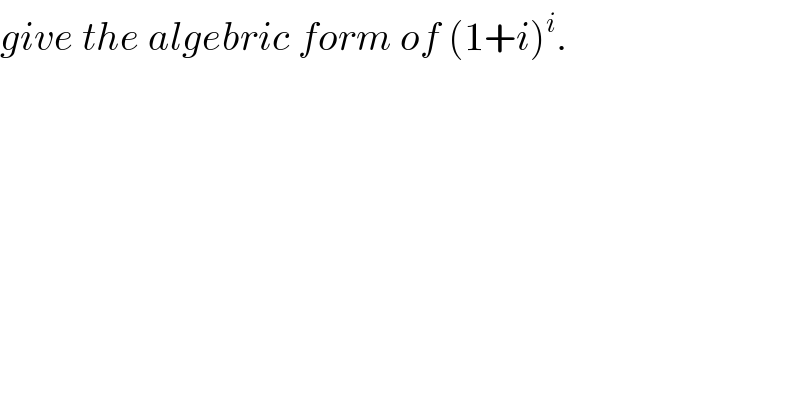
$${give}\:{the}\:{algebric}\:{form}\:{of}\:\left(\mathrm{1}+{i}\right)^{{i}} . \\ $$
Answered by MJS last updated on 28/Apr/18
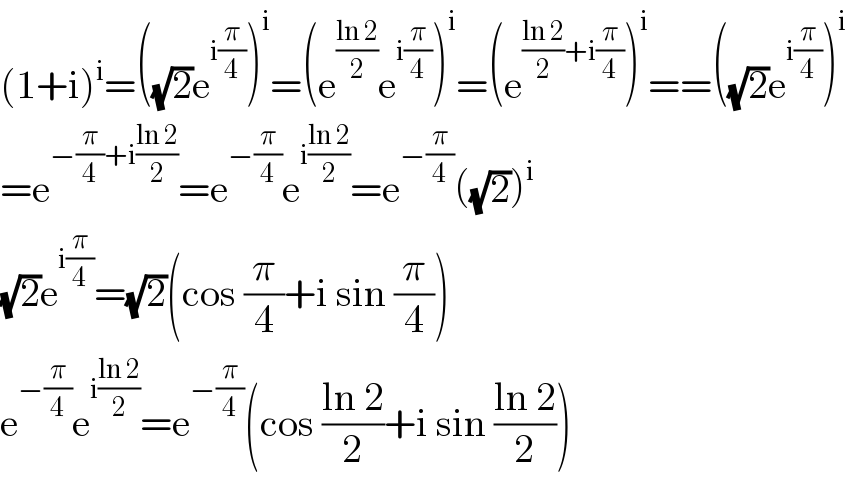
$$\left(\mathrm{1}+\mathrm{i}\right)^{\mathrm{i}} =\left(\sqrt{\mathrm{2}}\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)^{\mathrm{i}} =\left(\mathrm{e}^{\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}} \mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)^{\mathrm{i}} =\left(\mathrm{e}^{\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}+\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)^{\mathrm{i}} ==\left(\sqrt{\mathrm{2}}\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)^{\mathrm{i}} \\ $$$$=\mathrm{e}^{−\frac{\pi}{\mathrm{4}}+\mathrm{i}\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}} =\mathrm{e}^{−\frac{\pi}{\mathrm{4}}} \mathrm{e}^{\mathrm{i}\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}} =\mathrm{e}^{−\frac{\pi}{\mathrm{4}}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{i}} \\ $$$$\sqrt{\mathrm{2}}\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} =\sqrt{\mathrm{2}}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{4}}+\mathrm{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{e}^{−\frac{\pi}{\mathrm{4}}} \mathrm{e}^{\mathrm{i}\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}} =\mathrm{e}^{−\frac{\pi}{\mathrm{4}}} \left(\mathrm{cos}\:\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}+\mathrm{i}\:\mathrm{sin}\:\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$
