
Question Number 216918 by mathocean1 last updated on 24/Feb/25
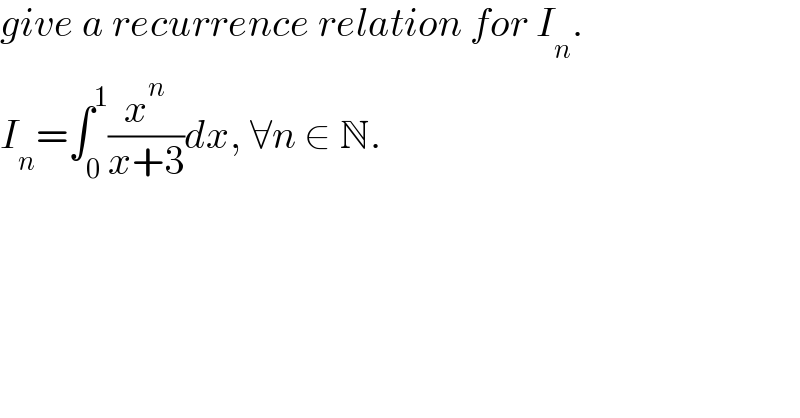
$${give}\:{a}\:{recurrence}\:{relation}\:{for}\:{I}_{{n}} . \\ $$$${I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} }{{x}+\mathrm{3}}{dx},\:\forall{n}\:\in\:\mathbb{N}. \\ $$
Answered by Wuji last updated on 24/Feb/25
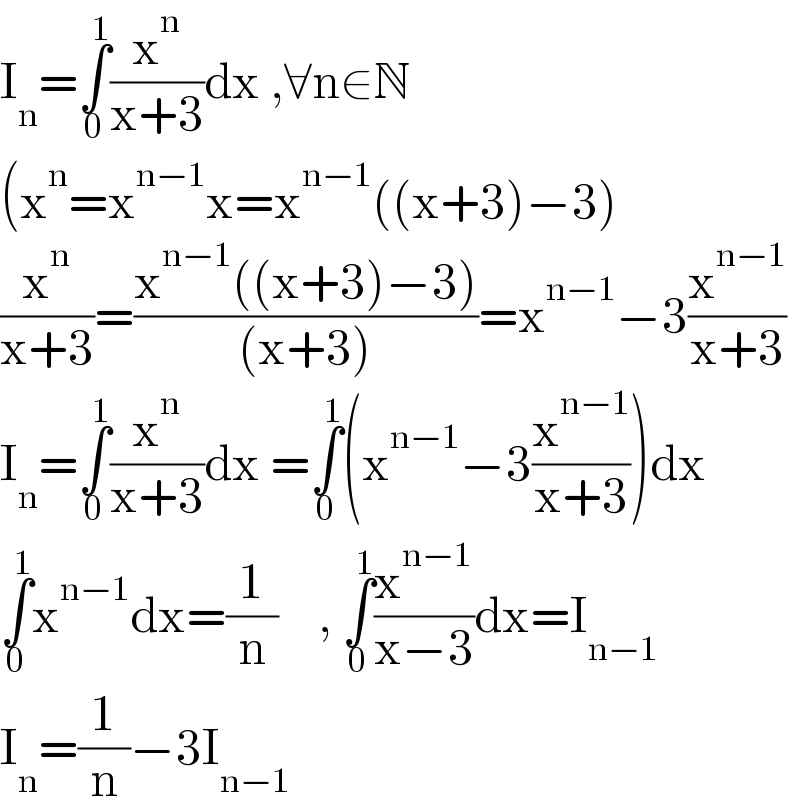
$$\mathrm{I}_{\mathrm{n}} =\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{x}+\mathrm{3}}\mathrm{dx}\:,\forall\mathrm{n}\in\mathbb{N} \\ $$$$\left(\mathrm{x}^{\mathrm{n}} =\mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{x}=\mathrm{x}^{\mathrm{n}−\mathrm{1}} \left(\left(\mathrm{x}+\mathrm{3}\right)−\mathrm{3}\right)\right. \\ $$$$\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{x}+\mathrm{3}}=\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} \left(\left(\mathrm{x}+\mathrm{3}\right)−\mathrm{3}\right)}{\left(\mathrm{x}+\mathrm{3}\right)}=\mathrm{x}^{\mathrm{n}−\mathrm{1}} −\mathrm{3}\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{x}+\mathrm{3}} \\ $$$$\mathrm{I}_{\mathrm{n}} =\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{x}+\mathrm{3}}\mathrm{dx}\:=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{x}^{\mathrm{n}−\mathrm{1}} −\mathrm{3}\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{x}+\mathrm{3}}\right)\mathrm{dx} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{dx}=\frac{\mathrm{1}}{\mathrm{n}}\:\:\:\:,\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{x}−\mathrm{3}}\mathrm{dx}=\mathrm{I}_{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{3I}_{\mathrm{n}−\mathrm{1}} \\ $$
Commented by mathocean1 last updated on 24/Feb/25

$${Thank}\:{you}\:{sir}... \\ $$
