
Previous in Relation and Functions Next in Relation and Functions
Question Number 92267 by mathmax by abdo last updated on 05/May/20
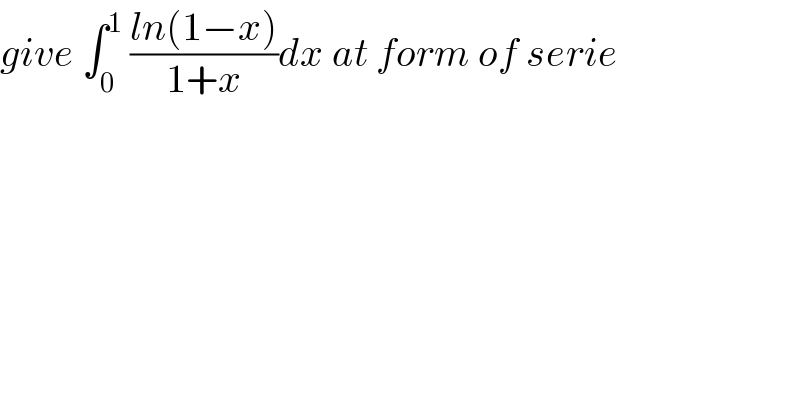
$${give}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}{dx}\:{at}\:{form}\:{of}\:{serie} \\ $$
Commented by mathmax by abdo last updated on 07/May/20
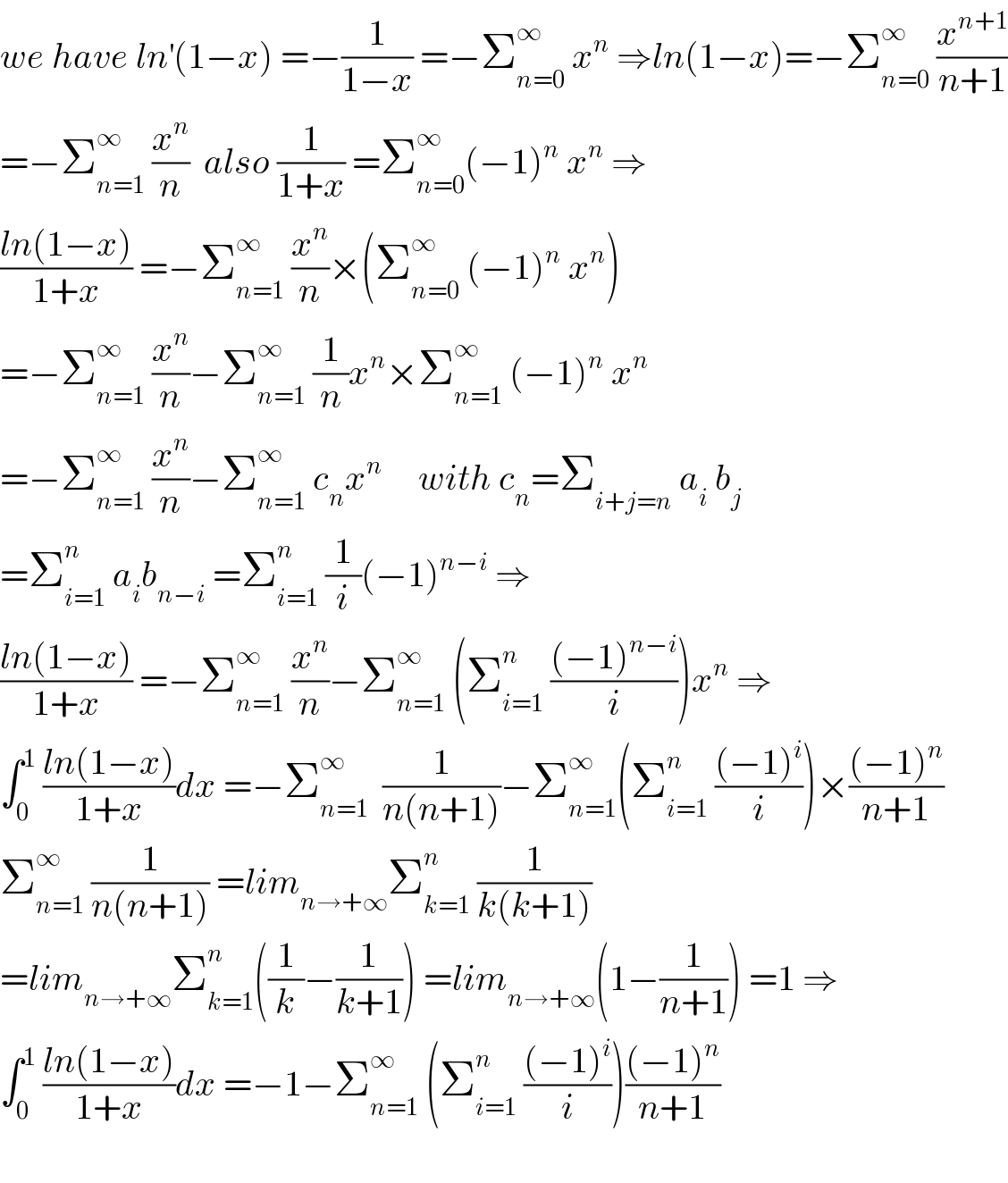
$${we}\:{have}\:{ln}^{'} \left(\mathrm{1}−{x}\right)\:=−\frac{\mathrm{1}}{\mathrm{1}−{x}}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \:\Rightarrow{ln}\left(\mathrm{1}−{x}\right)=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:\:{also}\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \:\Rightarrow \\ $$$$\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}×\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \right) \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}{x}^{{n}} ×\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}−\sum_{{n}=\mathrm{1}} ^{\infty} \:{c}_{{n}} {x}^{{n}} \:\:\:\:\:{with}\:{c}_{{n}} =\sum_{{i}+{j}={n}} \:{a}_{{i}} \:{b}_{{j}} \\ $$$$=\sum_{{i}=\mathrm{1}} ^{{n}} \:{a}_{{i}} {b}_{{n}−{i}} \:=\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{i}}\left(−\mathrm{1}\right)^{{n}−{i}} \:\Rightarrow \\ $$$$\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}−\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{n}−{i}} }{{i}}\right){x}^{{n}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}{dx}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}−\sum_{{n}=\mathrm{1}} ^{\infty} \left(\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{i}} }{{i}}\right)×\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}\:={lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)} \\ $$$$={lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right)\:={lim}_{{n}\rightarrow+\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)\:=\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}{dx}\:=−\mathrm{1}−\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{i}} }{{i}}\right)\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}} \\ $$$$ \\ $$
