Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 123304 by mordo last updated on 24/Nov/20

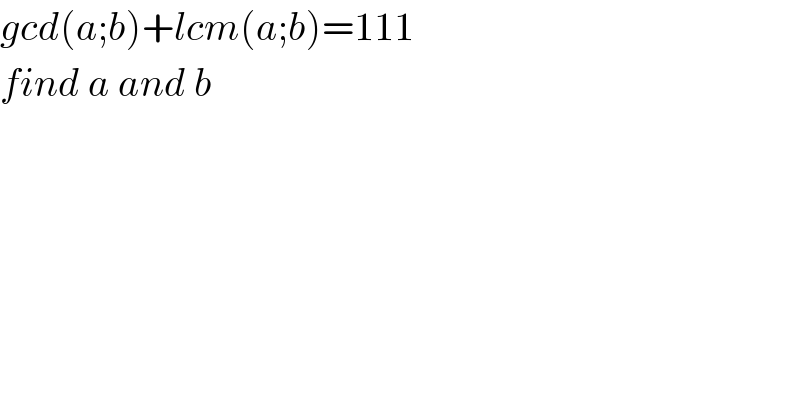
gcd(a;b)+lcm(a;b)=111 find a and b

$${gcd}\left({a};{b}\right)+{lcm}\left({a};{b}\right)=\mathrm{111} \\ $$$${find}\:{a}\:{and}\:{b} \\ $$

Commented by mr W last updated on 24/Nov/20

a=1 b=110

$${a}=\mathrm{1} \\ $$$${b}=\mathrm{110} \\ $$

Answered by MJS_new last updated on 24/Nov/20

(1) gcd (a, b) =1 ⇒ lcm (a, b) =ab=110 (2) gcd (a, b) =k≠1 ⇒ a=kx∧b=ky ⇒ ⇒ lcm (a, b) =kxy ⇒ k+kxy=111 ⇔ ⇔ k=((111)/(xy+1)) with gcd (x, y) =1 in both cases we can try to find solutions for a<b I get these pairs: a b 1 110 2 55 3 108 5 22 10 11 12 27 37 74

$$\left(\mathrm{1}\right)\:\mathrm{gcd}\:\left({a},\:{b}\right)\:=\mathrm{1}\:\Rightarrow\:\mathrm{lcm}\:\left({a},\:{b}\right)\:={ab}=\mathrm{110} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{gcd}\:\left({a},\:{b}\right)\:={k}\neq\mathrm{1}\:\Rightarrow\:{a}={kx}\wedge{b}={ky}\:\Rightarrow \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{lcm}\:\left({a},\:{b}\right)\:={kxy}\:\Rightarrow\:{k}+{kxy}=\mathrm{111}\:\Leftrightarrow \\ $$$$\:\:\:\:\:\Leftrightarrow\:{k}=\frac{\mathrm{111}}{{xy}+\mathrm{1}}\:\mathrm{with}\:\mathrm{gcd}\:\left({x},\:{y}\right)\:=\mathrm{1} \\ $$$$\mathrm{in}\:\mathrm{both}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{can}\:\mathrm{try}\:\mathrm{to}\:\mathrm{find}\:\mathrm{solutions} \\ $$$$\mathrm{for}\:{a}<{b}\:\mathrm{I}\:\mathrm{get}\:\mathrm{these}\:\mathrm{pairs}: \\ $$$${a}\:\:\:\:\:{b} \\ $$$$\mathrm{1}\:\:\:\:\:\mathrm{110} \\ $$$$\mathrm{2}\:\:\:\:\:\mathrm{55} \\ $$$$\mathrm{3}\:\:\:\:\:\mathrm{108} \\ $$$$\mathrm{5}\:\:\:\:\:\mathrm{22} \\ $$$$\mathrm{10}\:\:\:\mathrm{11} \\ $$$$\mathrm{12}\:\:\:\mathrm{27} \\ $$$$\mathrm{37}\:\:\:\mathrm{74} \\ $$

Answered by floor(10²Eta[1]) last updated on 24/Nov/20

let d=gcd(a, b)⇒a=dx, b=dy where gcd(x, y)=1 d+dxy=111∴d(1+xy)=111 d∣111⇒d=1, 3, 37, 111 Case 1: d=1⇒xy=ab=110=11.5.2 a=11.5.2, b=1 a=11.5, b=2 a=11.2, b=5 a=11, b=2.5 Case 2: d=3⇒xy=36=2^2 .3^2 x=2^2 .3^2 , y=1⇒a=2^2 .3^3 , b=3 x=3^2 , y=2^2 ⇒a=3^3 , b=2^2 .3 Case 3: d=37⇒xy=2 x=2, y=1⇒a=37.2, b=37 Case 4: d=111 (no sol.) (a, b)={(110, 1), (55, 2), (22, 5), (11, 10) (108, 3), (27,12), (74, 37)} and the (b, a) pairs

$$\mathrm{let}\:\mathrm{d}=\mathrm{gcd}\left(\mathrm{a},\:\mathrm{b}\right)\Rightarrow\mathrm{a}=\mathrm{dx},\:\mathrm{b}=\mathrm{dy} \\ $$$$\mathrm{where}\:\mathrm{gcd}\left(\mathrm{x},\:\mathrm{y}\right)=\mathrm{1} \\ $$$$\mathrm{d}+\mathrm{dxy}=\mathrm{111}\therefore\mathrm{d}\left(\mathrm{1}+\mathrm{xy}\right)=\mathrm{111} \\ $$$$\mathrm{d}\mid\mathrm{111}\Rightarrow\mathrm{d}=\mathrm{1},\:\mathrm{3},\:\mathrm{37},\:\mathrm{111} \\ $$$$\mathrm{Case}\:\mathrm{1}:\:\mathrm{d}=\mathrm{1}\Rightarrow\mathrm{xy}=\mathrm{ab}=\mathrm{110}=\mathrm{11}.\mathrm{5}.\mathrm{2} \\ $$$$\mathrm{a}=\mathrm{11}.\mathrm{5}.\mathrm{2},\:\mathrm{b}=\mathrm{1} \\ $$$$\mathrm{a}=\mathrm{11}.\mathrm{5},\:\mathrm{b}=\mathrm{2} \\ $$$$\mathrm{a}=\mathrm{11}.\mathrm{2},\:\mathrm{b}=\mathrm{5} \\ $$$$\mathrm{a}=\mathrm{11},\:\mathrm{b}=\mathrm{2}.\mathrm{5} \\ $$$$\mathrm{Case}\:\mathrm{2}:\:\mathrm{d}=\mathrm{3}\Rightarrow\mathrm{xy}=\mathrm{36}=\mathrm{2}^{\mathrm{2}} .\mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{x}=\mathrm{2}^{\mathrm{2}} .\mathrm{3}^{\mathrm{2}} ,\:\mathrm{y}=\mathrm{1}\Rightarrow\mathrm{a}=\mathrm{2}^{\mathrm{2}} .\mathrm{3}^{\mathrm{3}} ,\:\mathrm{b}=\mathrm{3} \\ $$$$\mathrm{x}=\mathrm{3}^{\mathrm{2}} ,\:\mathrm{y}=\mathrm{2}^{\mathrm{2}} \Rightarrow\mathrm{a}=\mathrm{3}^{\mathrm{3}} ,\:\mathrm{b}=\mathrm{2}^{\mathrm{2}} .\mathrm{3} \\ $$$$\mathrm{Case}\:\mathrm{3}:\:\mathrm{d}=\mathrm{37}\Rightarrow\mathrm{xy}=\mathrm{2} \\ $$$$\mathrm{x}=\mathrm{2},\:\mathrm{y}=\mathrm{1}\Rightarrow\mathrm{a}=\mathrm{37}.\mathrm{2},\:\mathrm{b}=\mathrm{37} \\ $$$$\mathrm{Case}\:\mathrm{4}:\:\mathrm{d}=\mathrm{111}\:\left(\mathrm{no}\:\mathrm{sol}.\right) \\ $$$$\left(\mathrm{a},\:\mathrm{b}\right)=\left\{\left(\mathrm{110},\:\mathrm{1}\right),\:\left(\mathrm{55},\:\mathrm{2}\right),\:\left(\mathrm{22},\:\mathrm{5}\right),\:\left(\mathrm{11},\:\mathrm{10}\right)\right. \\ $$$$\left.\left(\mathrm{108},\:\mathrm{3}\right),\:\left(\mathrm{27},\mathrm{12}\right),\:\left(\mathrm{74},\:\mathrm{37}\right)\right\} \\ $$$$\mathrm{and}\:\mathrm{the}\:\left(\mathrm{b},\:\mathrm{a}\right)\:\mathrm{pairs} \\ $$

Commented by mordo last updated on 25/Nov/20

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com