
Question Number 35513 by Rio Mike last updated on 19/May/18

$${g}\left({x}\right)=\:\mathrm{6}{x}^{\mathrm{2}} −\:\mathrm{5}{ax}\:+\:{b}^{\mathrm{2}} \\ $$$${given}\:{that}\:{g}\left({x}\right)\:{has}\:{only}\:{two}\:{roots} \\ $$$${and}\:{are}\:\left({x}−\mathrm{1}\right)\:{and}\:\left({x}−\mathrm{2}\right) \\ $$$${find}\:{the}\:{value}\:{of}\:{a}\:{and}\:{b}.{Using} \\ $$$$\left({x}−\mathrm{1}\right)\:{as}\:{a}\:{root}\:{detemine}\:{the}\: \\ $$$${extend}\:{to}\:{which}\:\left({x}−\mathrm{2}\right)\:{is}\:{a}\:{root} \\ $$$$\left({occurance}\:{as}\:{a}\:{root}\right). \\ $$
Answered by Rasheed.Sindhi last updated on 19/May/18
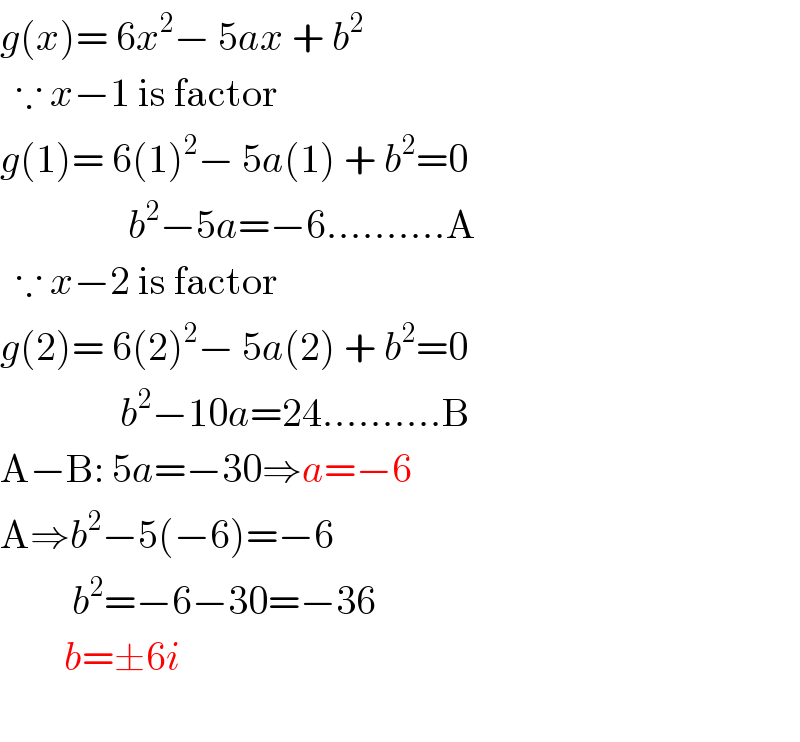
$${g}\left({x}\right)=\:\mathrm{6}{x}^{\mathrm{2}} −\:\mathrm{5}{ax}\:+\:{b}^{\mathrm{2}} \\ $$$$\:\:\because\:{x}−\mathrm{1}\:\mathrm{is}\:\mathrm{factor} \\ $$$${g}\left(\mathrm{1}\right)=\:\mathrm{6}\left(\mathrm{1}\right)^{\mathrm{2}} −\:\mathrm{5}{a}\left(\mathrm{1}\right)\:+\:{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}^{\mathrm{2}} −\mathrm{5}{a}=−\mathrm{6}..........\mathrm{A} \\ $$$$\:\:\because\:{x}−\mathrm{2}\:\mathrm{is}\:\mathrm{factor} \\ $$$${g}\left(\mathrm{2}\right)=\:\mathrm{6}\left(\mathrm{2}\right)^{\mathrm{2}} −\:\mathrm{5}{a}\left(\mathrm{2}\right)\:+\:{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}^{\mathrm{2}} −\mathrm{10}{a}=\mathrm{24}..........\mathrm{B} \\ $$$$\mathrm{A}−\mathrm{B}:\:\mathrm{5}{a}=−\mathrm{30}\Rightarrow{a}=−\mathrm{6} \\ $$$$\mathrm{A}\Rightarrow{b}^{\mathrm{2}} −\mathrm{5}\left(−\mathrm{6}\right)=−\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:{b}^{\mathrm{2}} =−\mathrm{6}−\mathrm{30}=−\mathrm{36} \\ $$$$\:\:\:\:\:\:\:\:{b}=\pm\mathrm{6}{i} \\ $$$$ \\ $$
