
Question Number 186503 by mnjuly1970 last updated on 05/Feb/23
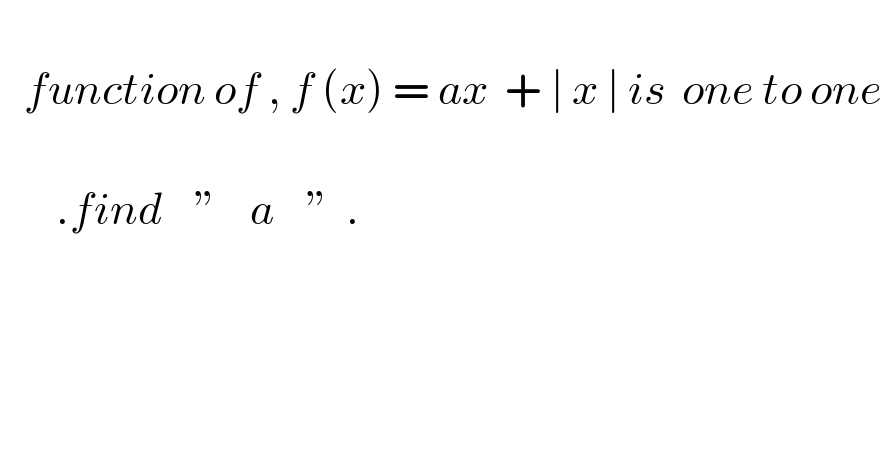
$$ \\ $$$$\:\:\:{function}\:{of}\:,\:{f}\:\left({x}\right)\:=\:{ax}\:\:+\:\mid\:{x}\:\mid\:{is}\:\:{one}\:{to}\:{one} \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:.{find}\:\:\:\:''\:\:\:\:{a}\:\:\:\:''\:\:. \\ $$$$\:\: \\ $$
Commented by Frix last updated on 05/Feb/23
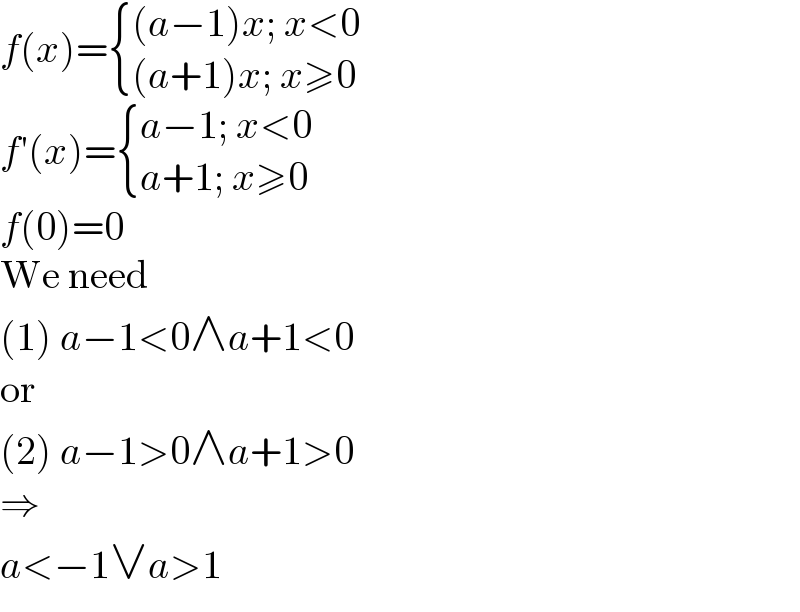
$${f}\left({x}\right)=\begin{cases}{\left({a}−\mathrm{1}\right){x};\:{x}<\mathrm{0}}\\{\left({a}+\mathrm{1}\right){x};\:{x}\geqslant\mathrm{0}}\end{cases} \\ $$$${f}'\left({x}\right)=\begin{cases}{{a}−\mathrm{1};\:{x}<\mathrm{0}}\\{{a}+\mathrm{1};\:{x}\geqslant\mathrm{0}}\end{cases} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{We}\:\mathrm{need} \\ $$$$\left(\mathrm{1}\right)\:{a}−\mathrm{1}<\mathrm{0}\wedge{a}+\mathrm{1}<\mathrm{0} \\ $$$$\mathrm{or} \\ $$$$\left(\mathrm{2}\right)\:{a}−\mathrm{1}>\mathrm{0}\wedge{a}+\mathrm{1}>\mathrm{0} \\ $$$$\Rightarrow \\ $$$${a}<−\mathrm{1}\vee{a}>\mathrm{1} \\ $$
