
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 103294 by bramlex last updated on 14/Jul/20

$$\mathrm{from}\:\mathrm{letters}\:\mathrm{in} \\ $$$$'\mathrm{MATEMATIKA}'\:\mathrm{words} \\ $$$$\mathrm{formed}\:\mathrm{by}\:\mathrm{using}\:\mathrm{all}\:\mathrm{the}\:\mathrm{letters}\:. \\ $$$$\mathrm{How}\:\mathrm{many}\:\mathrm{words}\:\mathrm{that}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{formed}\:\mathrm{with}\:\mathrm{the}\:\mathrm{five}\:\mathrm{consonant} \\ $$$$\mathrm{are}\:\mathrm{always}\:\mathrm{side}\:\mathrm{by}\:\mathrm{side}\: \\ $$
Answered by bemath last updated on 14/Jul/20
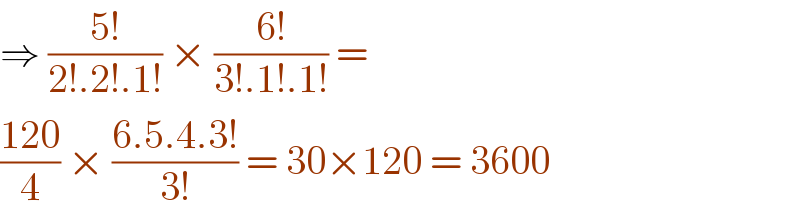
$$\Rightarrow\:\frac{\mathrm{5}!}{\mathrm{2}!.\mathrm{2}!.\mathrm{1}!}\:×\:\frac{\mathrm{6}!}{\mathrm{3}!.\mathrm{1}!.\mathrm{1}!}\:=\: \\ $$$$\frac{\mathrm{120}}{\mathrm{4}}\:×\:\frac{\mathrm{6}.\mathrm{5}.\mathrm{4}.\mathrm{3}!}{\mathrm{3}!}\:=\:\mathrm{30}×\mathrm{120}\:=\:\mathrm{3600} \\ $$
